A block of mass 2 kg slides on an intļined plane which makes an angle of 30 with the horizontal. The : efficient of friction between the block and the surface is $\sqrt{(3 / 2)}$
(a) What force should be applied to the block, so that the block moves down without any acceleration?
(b) What force should be applied to the block, so that it moves up without any acceleration ?
(c) Calculate the ratio of the powers needed in the above two cases, if the speed of block is same in both the cases.

Text Solution

Verified by Experts

$Here f_{L} = μ R = μ m g cos θ = μ m g cos θ = \sqrt{3 / 2} \times 2 \times g \times (\sqrt{3} / 2) = \frac{3 g}{\sqrt{2}}$
and component of weight alone the plane
$m g sin θ = 2 \times g \times (\frac{1}{2}) = g$
(a) As $m g sin θ < f_{L},$ the block will remain at rest on the plane and so to move it down the plane force F mu be applied parallel to the plane downwards as in figure (a).

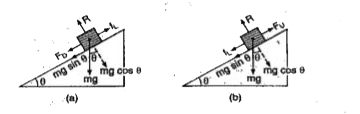
So, equation of motion down the plane will be
$(F_{D} + m g sin θ) - f_{L} = m a$
$or F_{D} + 2 g \frac{1}{2} = g \frac{3}{\sqrt{2}} [a s v = constant so, a = 0]$
$or F_{D} = (\frac{3 - \sqrt{2}}{\sqrt{2}}) g = 11 N$
(b) if $F_{U}$ is the force required to move the block up the plane, the equation of motion will be
$F_{υ} - (f_{L} + m g sin θ) = m a$
$or F_{υ} = 2 g \frac{1}{2} + g \frac{3}{\sqrt{2}} [as v = constant so,a = 0]$
$or F_{υ} = (\frac{3 + \sqrt{2}}{\sqrt{2}}) g = 30.6 N$
(c) As power $= (force) \times (velocity)$
$So, \frac{P_{D}}{P_{U}} = \frac{F_{D} v_{D}}{F_{υ} v_{υ}} = \frac{f_{D}}{F_{υ}} [as v_{D} = v_{υ}]$
$i . e ., \frac{P_{D}}{P_{υ}} = [\frac{3 - \sqrt{2}}{3 + \sqrt{2}}] = 0.36$

Updated on:21/07/2023