Initially the capacitor is uncharged, find the charge on the capacitor as a function of time, if switch is closed at t=0.
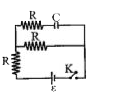
Method I : By applying KVL in loop (1)
As, ΣΔV=0
∴+ε−iR−i2R=0.....(10)
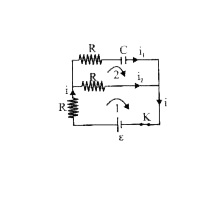
By applying KVL in loop (2)
As, ΣΔV=0
∴−i1R−qC+i2R=0.......(11)
Hence from both the equations, we can write an expression in terms of i1
From equation (10)
ε−(i1+i2)R−i2R=0
ε−i1R−2i2R=0
∴i2=ε−i1R2R.....(12)
From equations (11) and (12)
∴−i1R−qC+e−i1R2RR=0
−2i1R−2qC+ε−i1R=0,3i1R=ε−2qC
Again, we know that i1=dqdt
∴3dqdtR=ε−2qX⇒dqε−2qC=13Rdt
Integrating both sides,
∫q0dqε−2qC=∫t013Rdt.
1−2/C[ln(ε−2qC)]q0=13Rt
ln⎛⎜⎝ε−2qCε⎞⎟⎠=2t−3RC
ε−2qCε=e−2t/3RC, ε−2qC=εe−2t/3RC
ε−ε−2t/3RC=2qC, ε(1−e−2t/3RC)=2qC
q=Cε2(1−e−2t/3RC)
Method II Another method can be to find the charge on the capacitor of R-C circuit as a function of time Before going to the method - II, we need to learn a very important concept related to electrical circuit or network. This concept is not only used to solve the problems of R-C circuit but you apply it for any type of electrical circuit also. Consider the circuit as shown in the figure
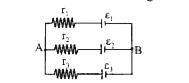
The circuit can be converted to a single source of battery by using the following formula
Equivalent emf, εeq=VA−VB=(ε1r1+ε2r2+ε3r3)(1r1+1r2+1r3).....(13)
Where ε1,ε2 and ε3 are the net emf of the branches 1,2 and 3 resistance respectively.
Internal resistance of the equivalent battery can be given by the following formula.
1req=1r1+1r2+1r3
Suppose we have to convert the given circuit into an equivalent battery where, ε1=3V,ε2=−2V,ε3=1V and r1=r2=r3=1Ω.
Equivalent emf of the battery can be written as,
εeq=VA−VB=(+31+−21++11)(11+11+11)=23V
Internal resistance of the equivalent battery can be given by following formula,
1req=1r1+1r2+1r3=1req=11+11+11∴req=13Ω
Hence the given network becomes as a single source of voltage 23V and having an internal resistance 13Ω
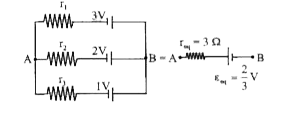
For problem related with R-C circuit with DC source, it is easier to convert the R-C circuit having a number of parallel branches into a R-C circuit of single voltage source with a series resistance. It makes the solution of complicated networks quite quick and easy.
Similar Questions
Knowledge Check
Initially the capacitor was uncharged Current in the capacitor just after switching on will be ?
 AεRBε2RCε5RDε4R
AεRBε2RCε5RDε4RThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
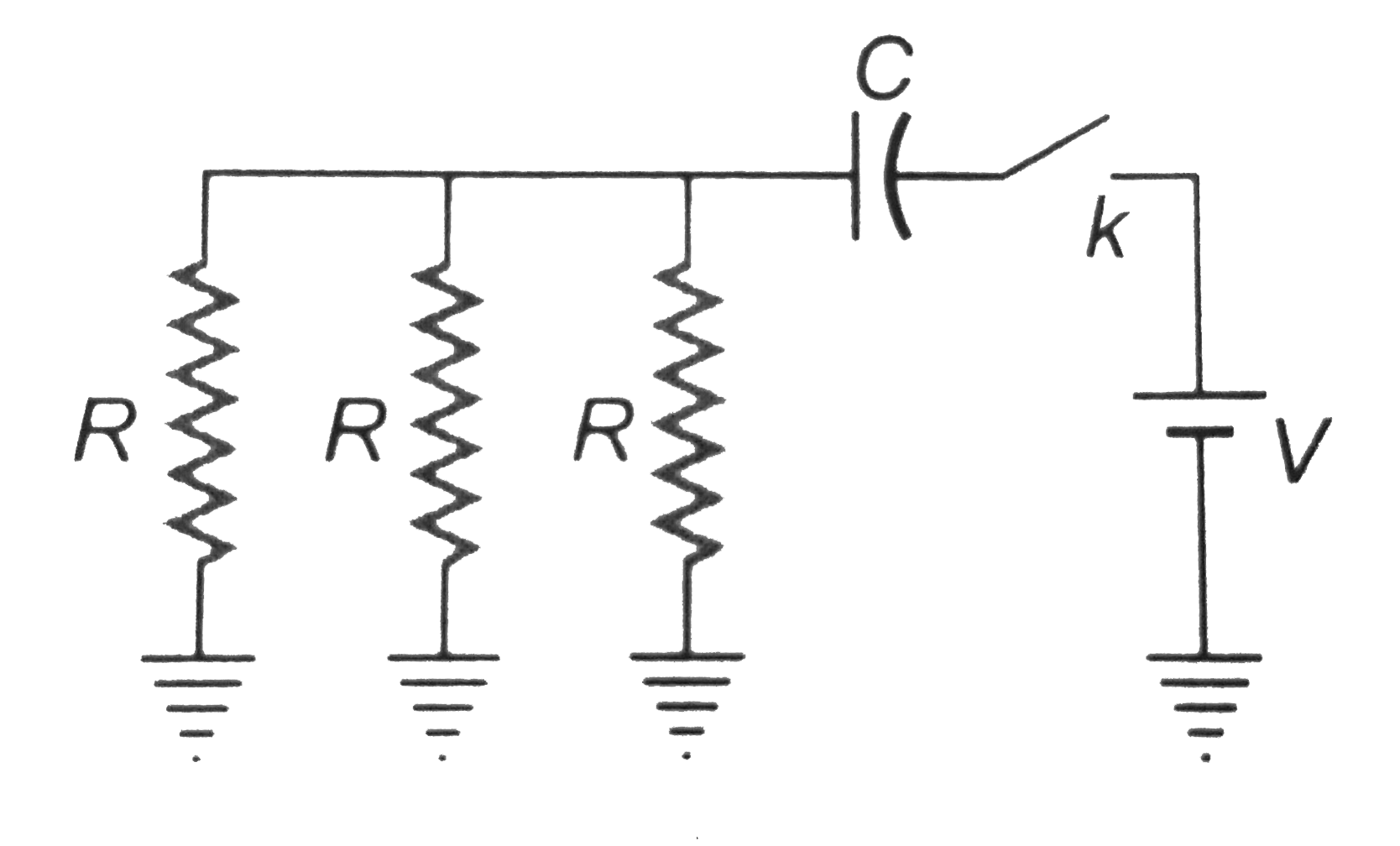 ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)
ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)
Initially the capacitor was uncharged Current in the capacitor just after switching on will be ?

View SolutionThe charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
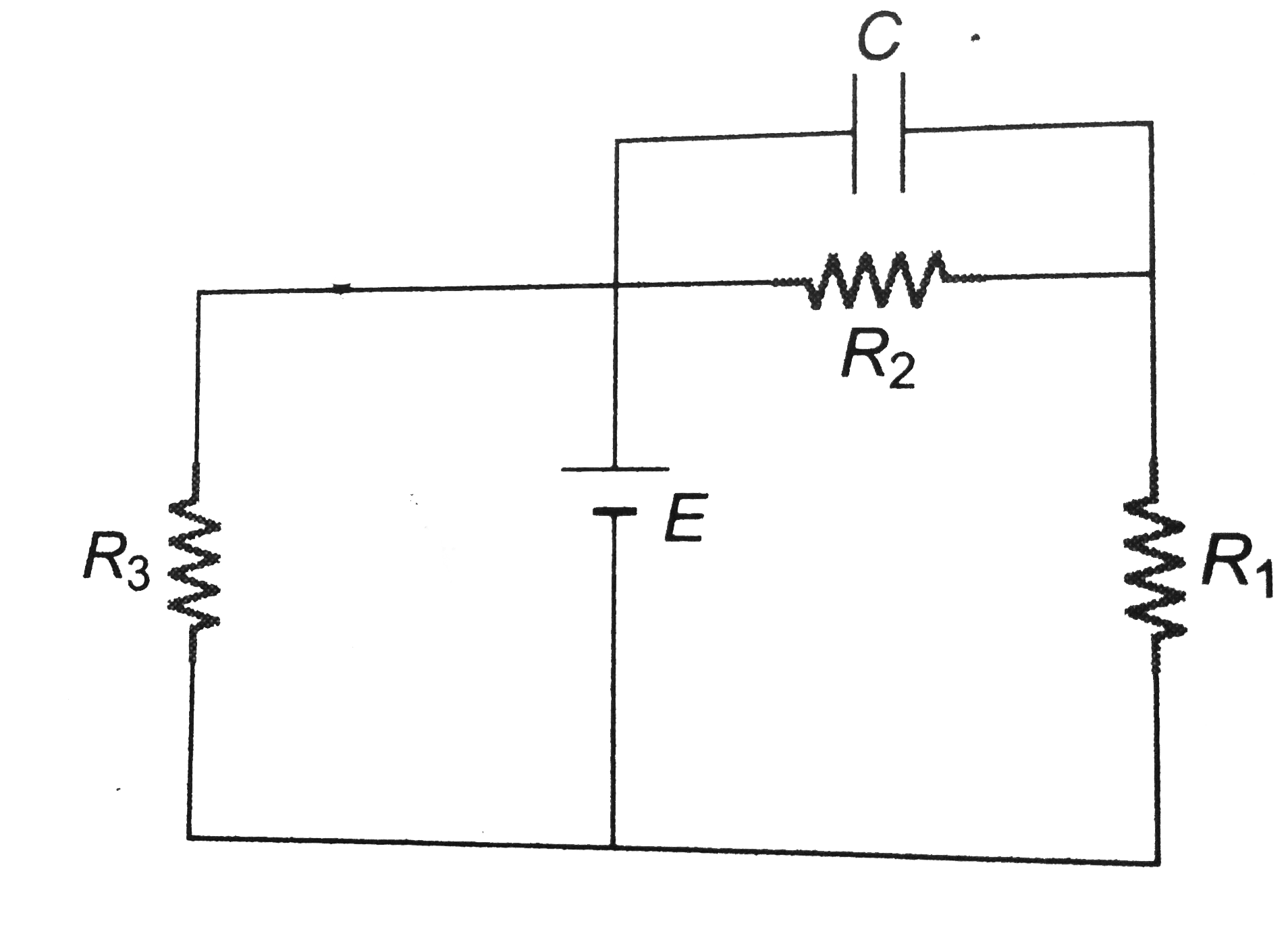
View SolutionThe charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.

View Solutioninitially the switch is open for a long time. Now the swithc is closed at t=0. find the caharge on the rightomost capacitor as a function of time given that it was initially unchanged.
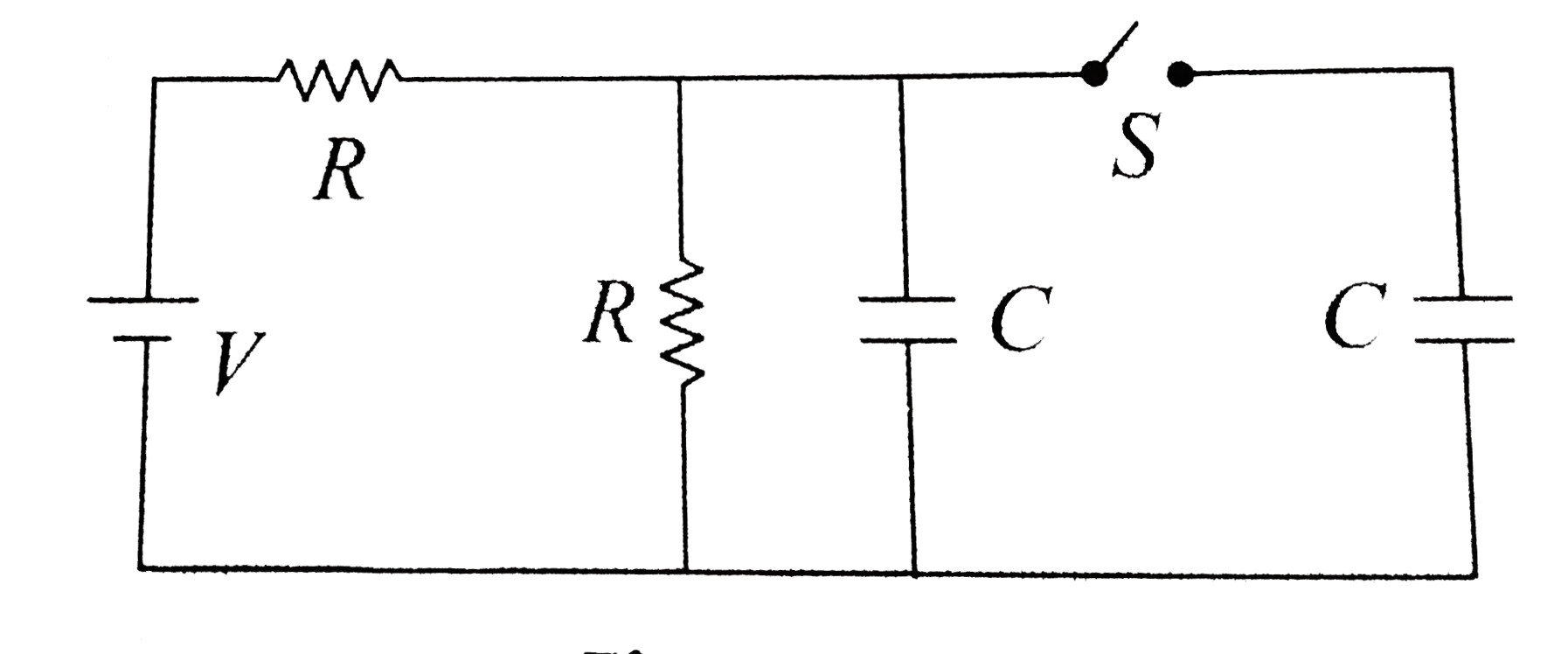
View Solutioninitially the switch is open for a long time. Now the swithc is closed at t=0. find the caharge on the rightomost capacitor as a function of time given that it was initially unchanged.

View SolutionThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by

View Solution

