A source of light of wavelength λ=500nm is placed in situation as shown in the figure. Considering interference of direct and reflected rays.
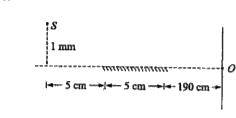
The shape of dark fringes on the screen is
hyperbolic
straight line
circular
none of these
Here, point source S and its image S. behave as coherent sources. SS. is parallel to screen , so shape will be hyperbolic.
Similar Questions
A source of light of wavelength 5000Å is placed as shown in figure.
Considering interference of direct and reflected rays, determine the position of the
region where the fringes will be visible and calculate the number of fringes.
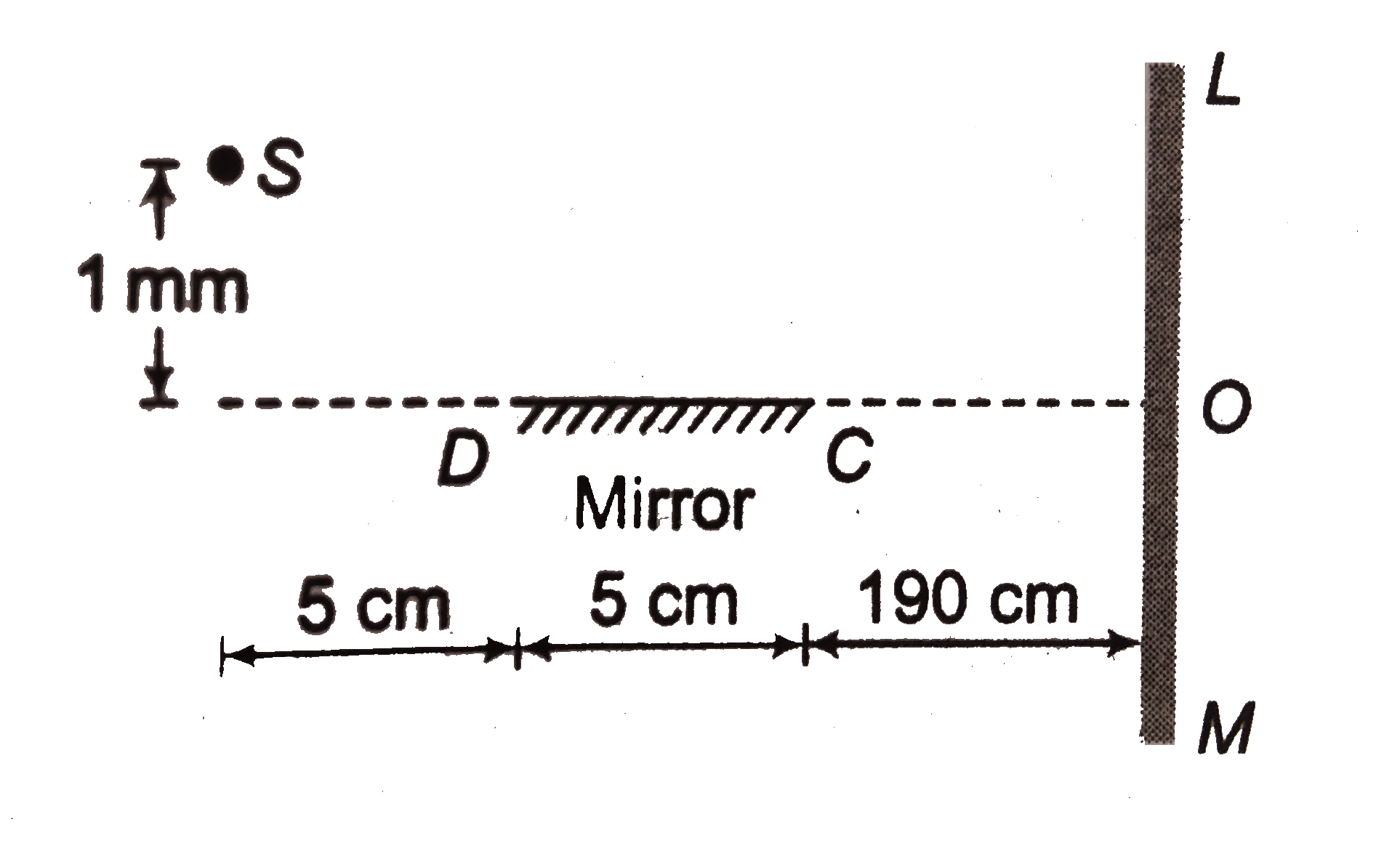 .
.
View SolutionA point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
View Solution
Knowledge Check
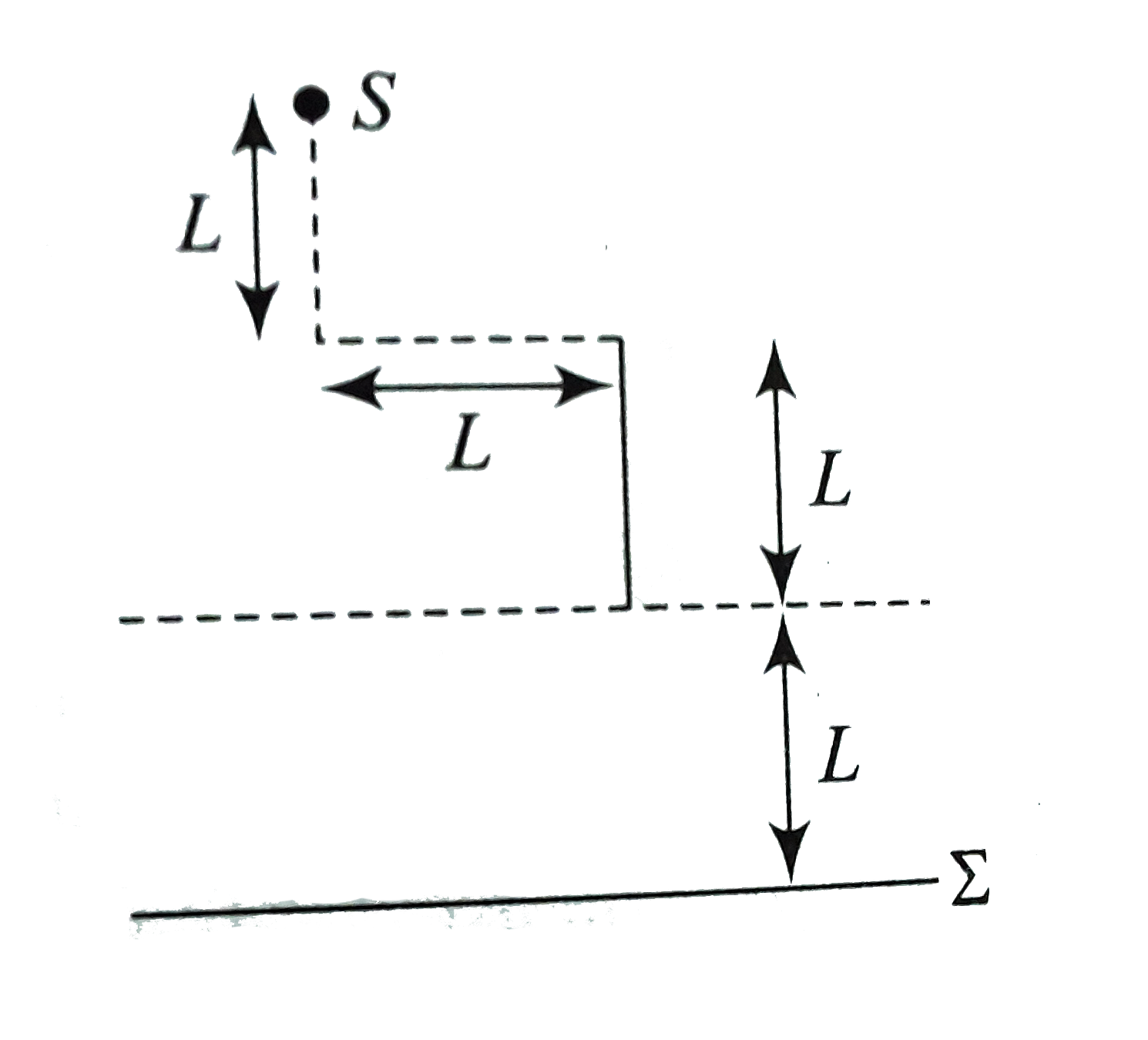
A point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
 ALB2LC3L/2DL/2
ALB2LC3L/2DL/2A monochromatic light source S of wavelength 440 nm is placed slightly above a plane mirror M as shown . Image of S in M can be used as a virtual source to produce interference fringes on the screen. The distance of source S from O is 20.0 cm, and the distance of screen from O is 100.0 cm (figure is not to scale). If the angle θ=0.50×10−3 radians, the width of the interference fringes observed on the screen is –
 A2.20 mmB2.64 mmC1.10 mmD0.55 mm
A2.20 mmB2.64 mmC1.10 mmD0.55 mmA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
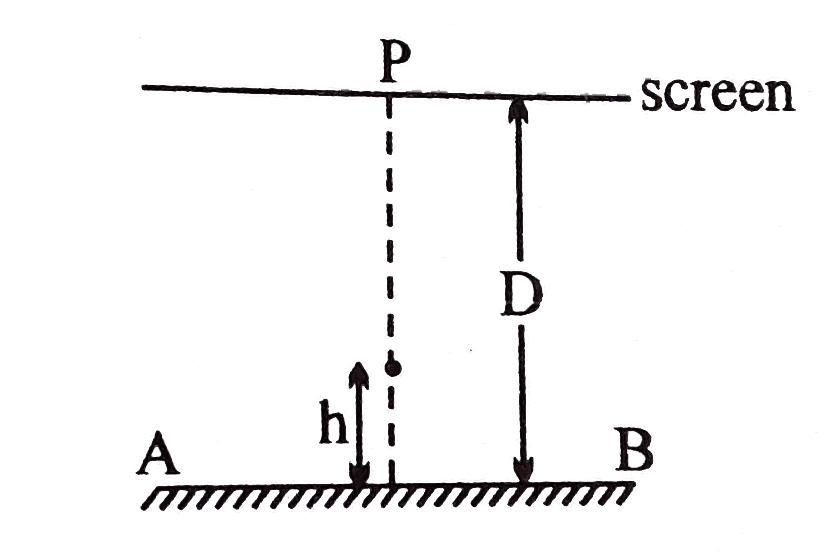
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.AcircleBsquareCparbolaDstraight line
(a) In Young's double slit experiment, a monochromatic source of light S is kept equidistant from the slits S1andS2. Explain the information of dark and bright fringes on the screen.
(b) A beam of light consisting of two wavelength, 650 nm and 520 nm, is used to obtain interference fringes in a Young's double - slit experiment.
(i) Find the distance of the third bright fringe on the screen from the central maximum for wavelengths 650 nm.
(ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide ?
Given: The seperation between the slits is 4 mm and the distance between the screen and plane of the slits is 1.2 m.
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
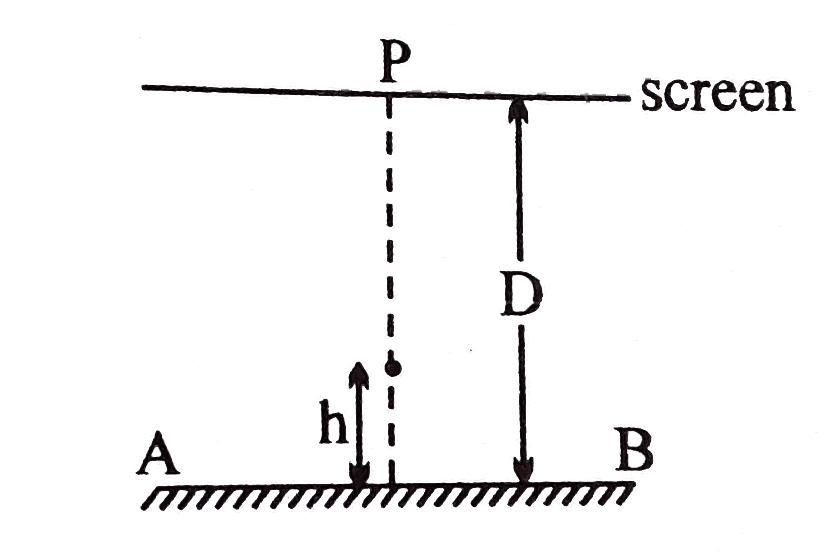
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
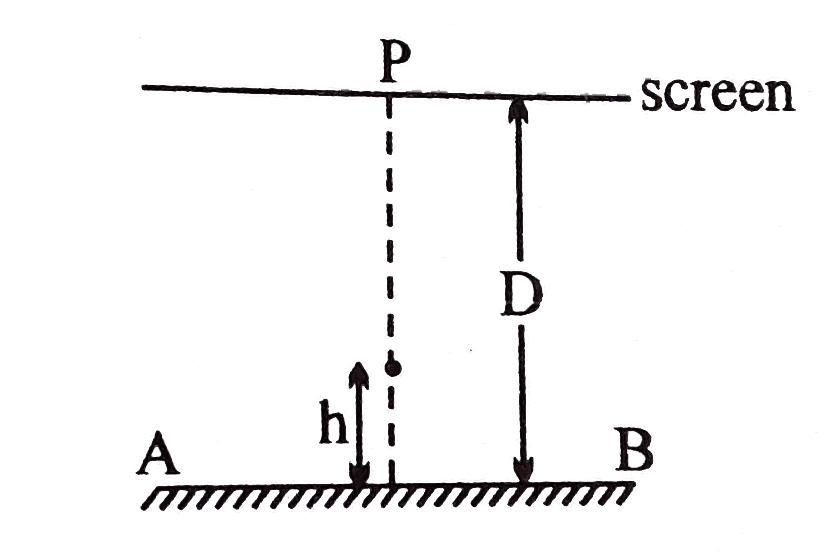
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is

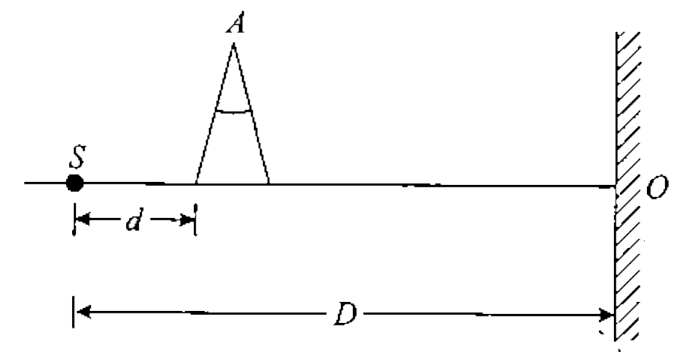
View SolutionA prism having angle A∘ (which is very small) is placed in front of a point source S at a small distance d. A screen is placed at a large distance D as shown in the figure-6.113. Find the fringe width of interference pattern given that source is emitting light of wavelength λ and refractive index of prism is μ.
View Solution
