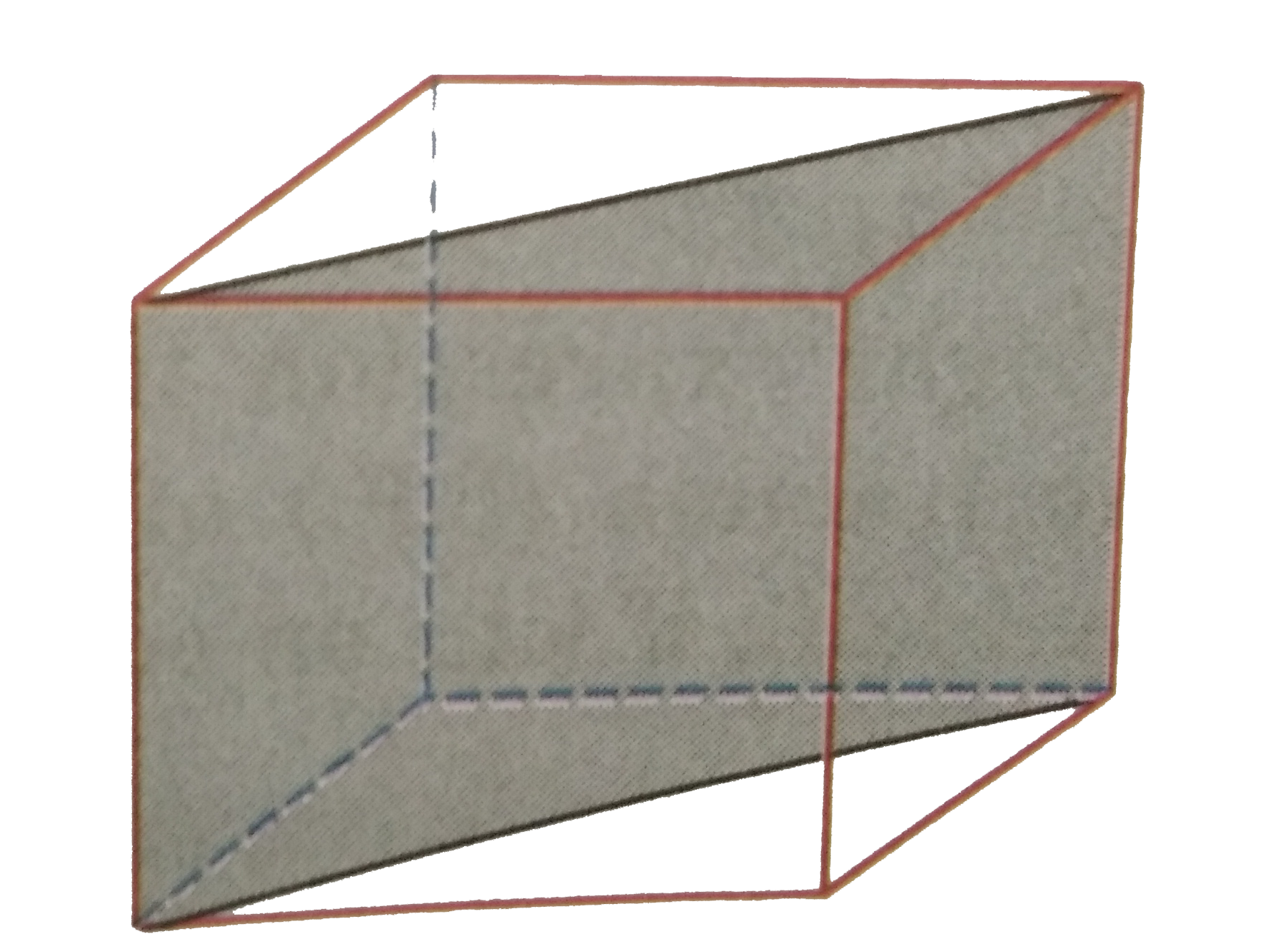
In a hypothetical solid, C atoms are found to form cubical close-packed lattice. A atoms occupy all tetrahedral voids and B atoms occupy all octahedral voids.

A and B atoms are of appropriate size, so that there is no distortion in the CCP lattice of C atoms. Now, if a plane as shown in the following figure is cut, then the cross section of this plane will look like



None of these
The correct Answer is:D
From figure, it is clear that 4 corners and 2 face centers lie on the shaded plane. Therefore, there will be six C atoms, and atoms (marked A) in TVs do not touch other.
Fig (i) is not possible, four atom marked
Fig. (ii) is not possible, atoms A in TVs are not shown in figure.
Fig. (iii) is not possible, since atoms B and C are not touching each other and sizes of TV and OV are equal.
Topper's Solved these Questions
Similar Questions
In a hypothetical solid C atoms form C C P lattice with A atoms occupying all the Tetrahedral Voids and B atoms occupying all the octahedral voids A and B atoms are of the appropriate size such that there is no distortions in the CCP lattice. Now if a plane is cut ( as shown ) then the section would like

View SolutionA forms ccp lattice B occupy half of the octahedral voids and O occupy all the tetrahedral voids. Calculate formula-
View Solution
Knowledge Check
In a hypothetical solid , C atoms are found to form cubical close - packed lattice . A atoms occupy all tetrahedral voids and B atoms occupy all octahedral voids .
A and B atoms are of appropriate size , so that there is no distortion in the ccp lattice of C atoms . Now if a plane as shown in the above figure is cut , then the cross section of this plane will look likeA B
B C
C D
D
In a hypothetical solid C atoms form C C P lattice with A atoms occupying all the Tetrahedral Voids and B atoms occupying all the octahedral voids A and B atoms are of the appropriate size such that there is no distortions in the CCP lattice. Now if a plane is cut ( as shown ) then the section would like
 A
A B
B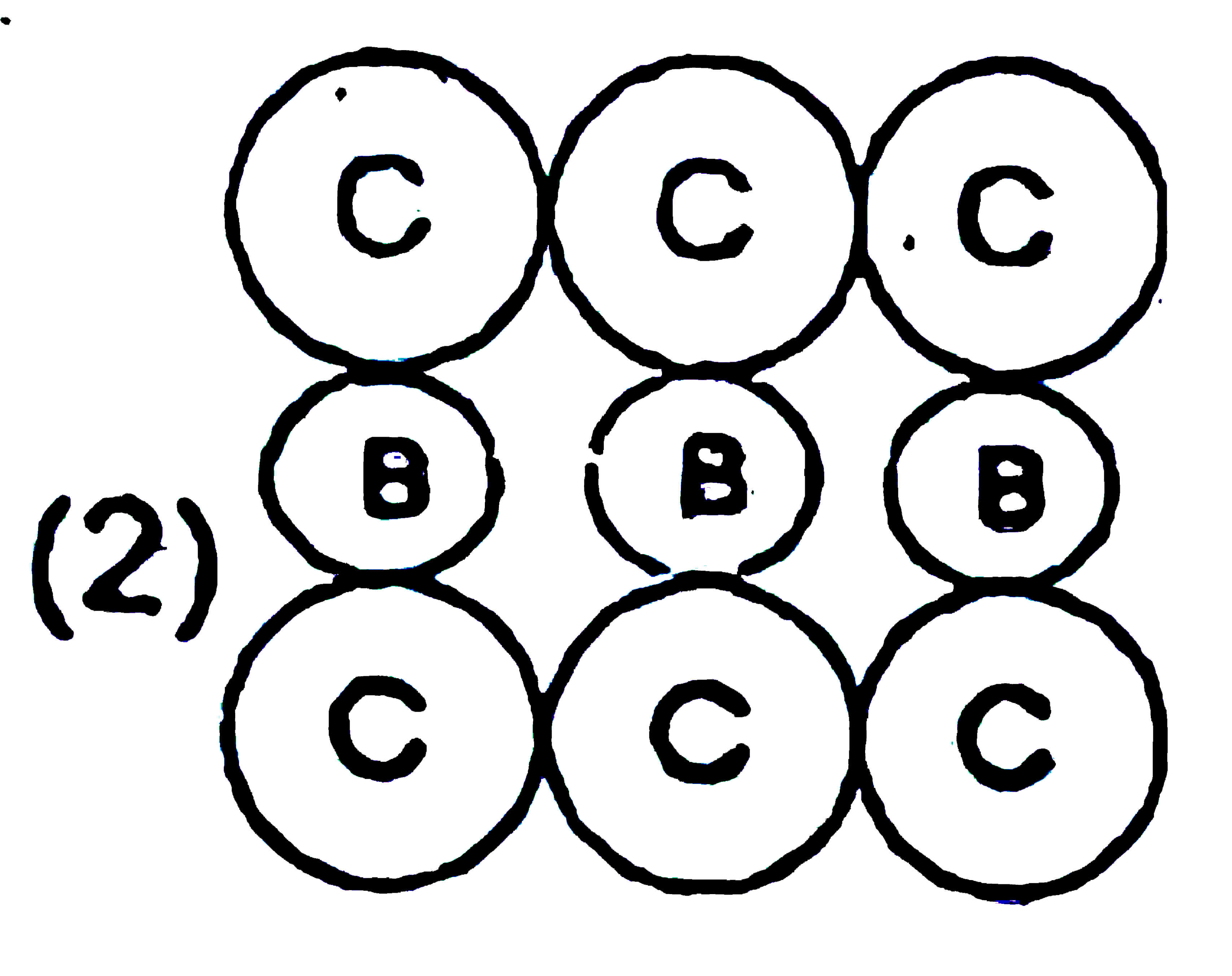 C
C D
D
Atoms A present in ccp lattice atoms B occupied tetrahedral voids and atoms C present in octahderal voids. The formula of compound is
AA2BCBABC2CAB2CDABC
A forms ccp lattice B occupy half of the octahedral voids and O occupy all the tetrahedral voids. Calculate formula-
View SolutionA solid is formed and it has three types of atoms X, Y and Z, X forms a fcc lattice with Y atoms occupying all tetrahedral voids and Z atoms occupying half of octahedral voids. The formula of solid is :-
View SolutionA solid is formed and it has three types of atoms X, Y and Z, X forms a fcc lattice with Y atoms occupying all tetrahedral voids and Z atoms occupying half of octahedral voids. The formula of solid is :-
View SolutionA solid is formed and it has three types of atoms X, Y and Z, X forms a fcc lattice with Y atoms occupying all tetrahedral voids and Z atoms occupying half of octahedral voids. The formula of solid is :-
View SolutionA solid is formed by three elements X,Y and Z, X atoms form a fcc lattice with Y atoms occupying all tetrahedral voids. Z atoms occupying half the octahedral voids. The formula of the solids is :
View Solution
