Define time constant of an RC circuit. What is its SI unit?
Step-by-Step Solution
1. Definition of Time Constant:
The time constant (denoted by the symbol τ, tau) of an RC (resistor-capacitor) circuit is defined as the time required for the charge on the capacitor to reach approximately 63.2% of its maximum value when charging, or to decay to about 36.8% of its initial value when discharging.
2. Charging Definition:
When charging, the time constant τ is the time taken for the capacitor to charge to 63.2% of the maximum charge (Q_max) it can hold. Mathematically, if Q is the charge at time t, then:
Q(t)=Qmax(1−e−t/τ)
At t=τ, Q(τ)=0.632×Qmax.
3. Discharging Definition:
When discharging, the time constant τ is the time taken for the charge on the capacitor to decrease to 36.8% of its initial charge (Q_initial). Mathematically, if Q is the charge at time t, then:
Q(t)=Qinitiale−t/τ
At t=τ, Q(τ)=0.368×Qinitial.
4. SI Unit of Time Constant:
The SI unit of the time constant τ is seconds (s), as it represents a time duration.
5. Expression for Time Constant:
The time constant can also be expressed in terms of resistance (R) and capacitance (C) of the circuit:
τ=R×C
where R is the resistance in ohms (Ω) and C is the capacitance in farads (F).
Summary
- The time constant τ of an RC circuit is the time required for a capacitor to charge to 63.2% of its maximum charge or discharge to 36.8% of its initial charge.
- The SI unit of the time constant is seconds (s).
- The time constant can be calculated using the formula τ=R×C.
The time constant (denoted by the symbol τ, tau) of an RC (resistor-capacitor) circuit is defined as the time required for the charge on the capacitor to reach approximately 63.2% of its maximum value when charging, or to decay to about 36.8% of its initial value when discharging.
When charging, the time constant τ is the time taken for the capacitor to charge to 63.2% of the maximum charge (Q_max) it can hold. Mathematically, if Q is the charge at time t, then:
Q(t)=Qmax(1−e−t/τ)
At t=τ, Q(τ)=0.632×Qmax.
When discharging, the time constant τ is the time taken for the charge on the capacitor to decrease to 36.8% of its initial charge (Q_initial). Mathematically, if Q is the charge at time t, then:
Q(t)=Qinitiale−t/τ
At t=τ, Q(τ)=0.368×Qinitial.
The SI unit of the time constant τ is seconds (s), as it represents a time duration.
The time constant can also be expressed in terms of resistance (R) and capacitance (C) of the circuit:
τ=R×C
where R is the resistance in ohms (Ω) and C is the capacitance in farads (F).
- The time constant τ of an RC circuit is the time required for a capacitor to charge to 63.2% of its maximum charge or discharge to 36.8% of its initial charge.
- The SI unit of the time constant is seconds (s).
- The time constant can be calculated using the formula τ=R×C.
Topper's Solved these Questions
- SAMPLE PAPER 2022BOOK - ICSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - PART II (SECTION B)
8 Videos
- SAMPLE PAPER 2022BOOK - ICSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - PART II (SECTION C)
8 Videos
- SAMPLE PAPER 2022BOOK - ICSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - PART I (Question)
15 Videos
Similar Questions
Define power. What is its Sl unit?
View SolutionDefine speed. What is its S.I. unit?
View SolutionDefine quality factor of resonance in series LCR circuit.What is its SI unit ?
View SolutionTwo identical resistors of magnitude R and two identical capacitors of magnitude C are used to form an RC circuit. In which case the time constant of the RC circuit is the highest?
View SolutionThe capacitive time constant of the RC circuit shown in the figure.
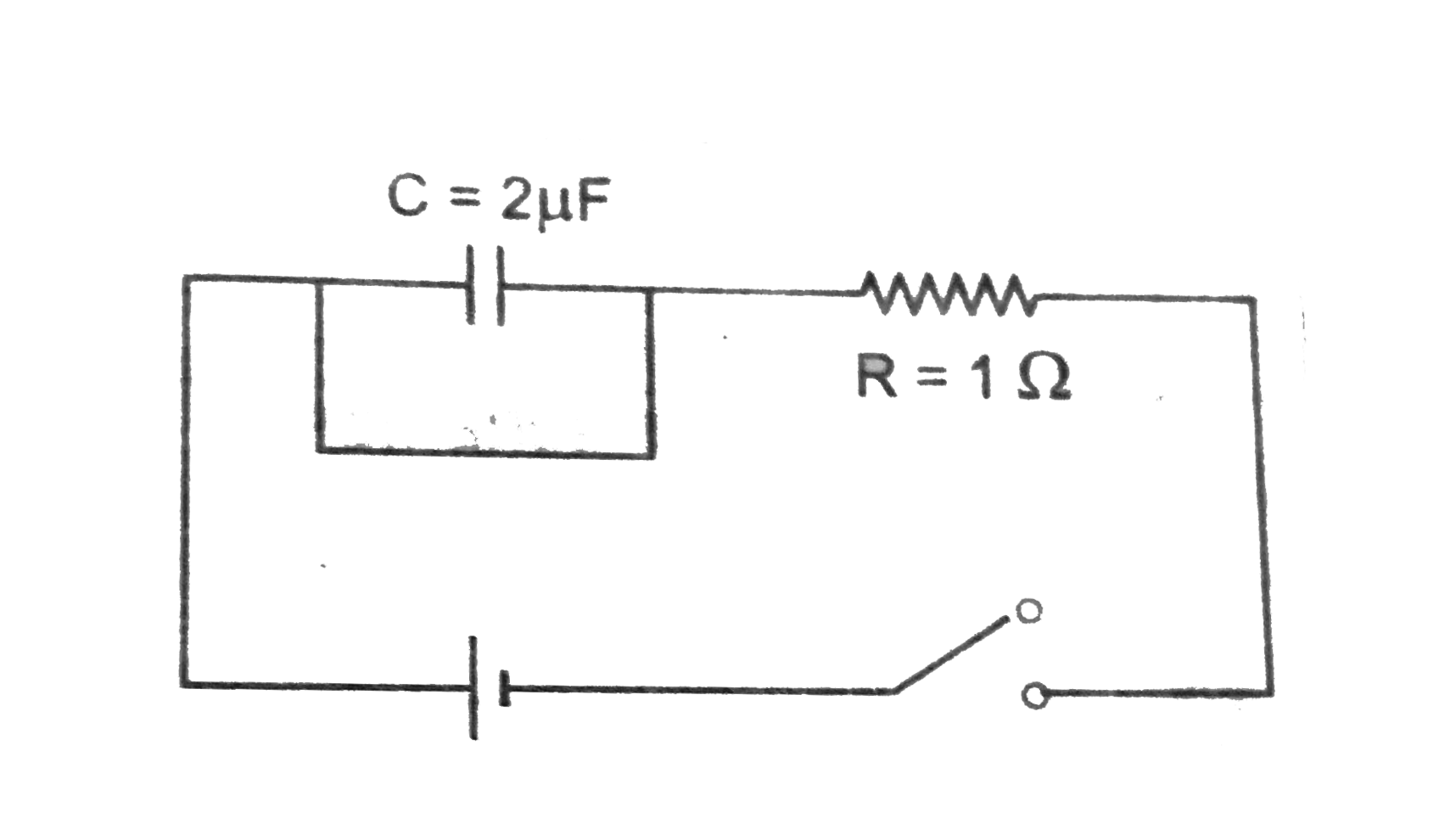
View SolutionDefine displacement. What is its S.I. unit?
View SolutionDefine electric current. What is its SI unit?
View SolutionDefine amplitude of a vibrating body. What is its SI unit?
View SolutionDefine temperature. What is its Sl unit?
View SolutionDefine the activity of a radionuclide. Write its SI unit. Give a plot of the activity of a radioactive species versus time.
View Solution
