Two identical resistors of magnitude R and two identical capacitors of magnitude C are used to form an RC circuit. In which case the time constant of the RC circuit is the highest?
Two resistors and two capacitors connected in series with a power supply.
Two resistors and two capacitors connected in parallel with a power supply.
Two resistors connected in parallel, two capacitors connected in parallel, and those two combinations are in series with a power supply
Two resistors connected in series, two capacitors connected in parallel and those two combinations are connected in series with a power supply.
The correct Answer is:D
To determine the configuration of two identical resistors (R) and two identical capacitors (C) that yields the highest time constant in an RC circuit, we can follow these steps:
Step 1: Understand the Time Constant Formula
The time constant (τ) for an RC circuit is given by the formula:
τ=Requivalent×Cequivalent
where Requivalent is the equivalent resistance and Cequivalent is the equivalent capacitance.
Step 2: Analyze the Resistor Configuration
To maximize the equivalent resistance:
- When resistors are connected in series, the equivalent resistance is:
Requivalent=R+R=2R
This configuration will yield the maximum resistance.
Step 3: Analyze the Capacitor Configuration
To maximize the equivalent capacitance:
- When capacitors are connected in parallel, the equivalent capacitance is:
Cequivalent=C+C=2C
This configuration will yield the maximum capacitance.
Step 4: Combine the Configurations
Now, we combine the two configurations:
- Connect the two resistors in series to get Requivalent=2R.
- Connect the two capacitors in parallel to get Cequivalent=2C.
Step 5: Calculate the Maximum Time Constant
Substituting the equivalent values into the time constant formula:
τ=Requivalent×Cequivalent=(2R)×(2C)=4RC
This shows that the time constant is maximized at 4RC.
Conclusion
To achieve the highest time constant in the RC circuit:
- The two resistors should be connected in series.
- The two capacitors should be connected in parallel.
- This combination should then be connected across a power supply.
Thus, the correct configuration for the highest time constant is:
Two resistors in series and two capacitors in parallel.
---
The time constant (τ) for an RC circuit is given by the formula:
τ=Requivalent×Cequivalent
where Requivalent is the equivalent resistance and Cequivalent is the equivalent capacitance.
To maximize the equivalent resistance:
- When resistors are connected in series, the equivalent resistance is:
Requivalent=R+R=2R
This configuration will yield the maximum resistance.
To maximize the equivalent capacitance:
- When capacitors are connected in parallel, the equivalent capacitance is:
Cequivalent=C+C=2C
This configuration will yield the maximum capacitance.
Now, we combine the two configurations:
- Connect the two resistors in series to get Requivalent=2R.
- Connect the two capacitors in parallel to get Cequivalent=2C.
Substituting the equivalent values into the time constant formula:
τ=Requivalent×Cequivalent=(2R)×(2C)=4RC
This shows that the time constant is maximized at 4RC.
To achieve the highest time constant in the RC circuit:
- The two resistors should be connected in series.
- The two capacitors should be connected in parallel.
- This combination should then be connected across a power supply.
Two resistors in series and two capacitors in parallel.
Similar Questions
The time constant of C-R circuit is
View SolutionThe capacitive time constant of the RC circuit shown in the figure.
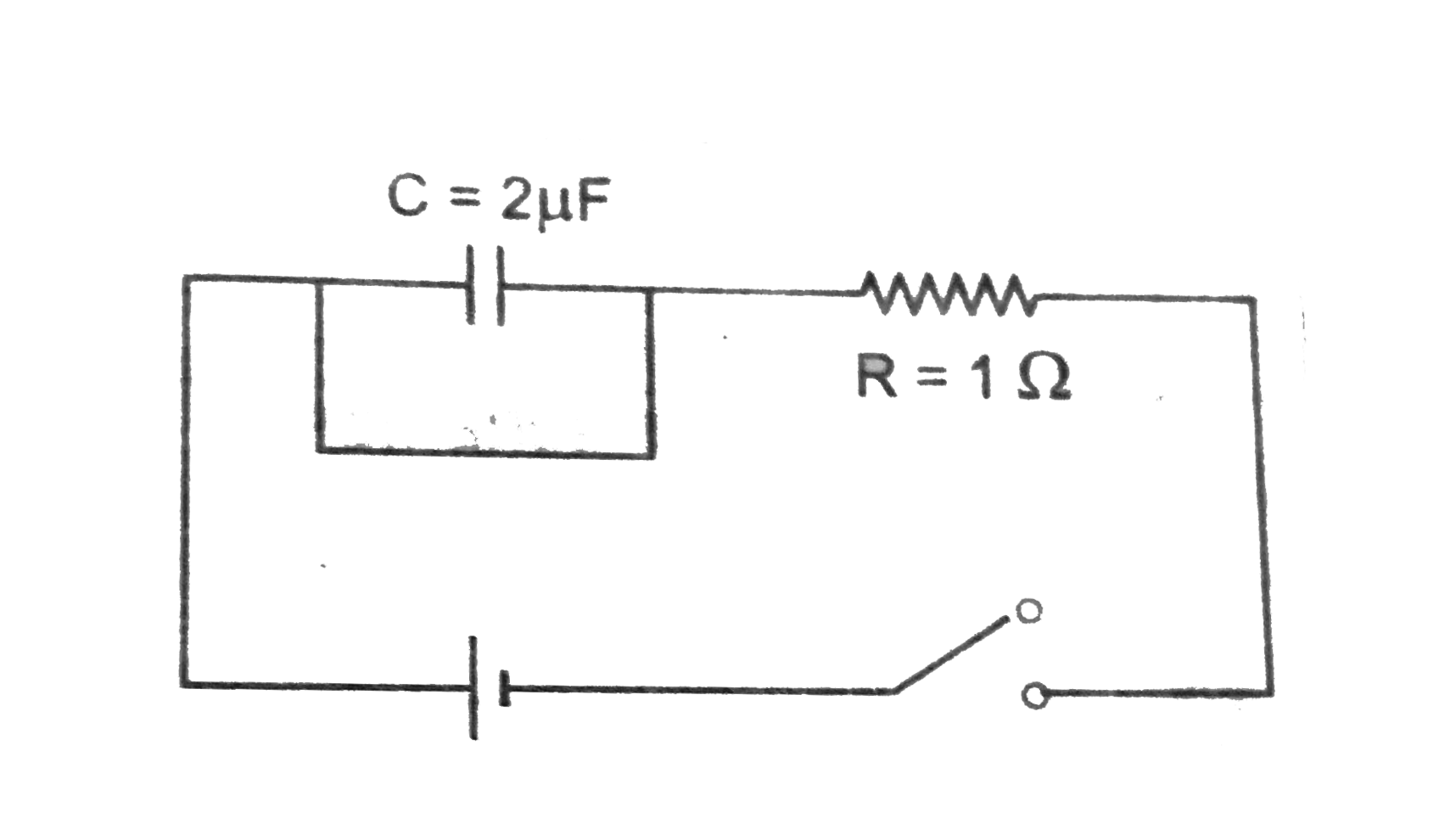
View SolutionDefine time constant of an RC circuit. What is its SI unit?
View SolutionThe figure shows an experimental plot discharging of a capacitor in an RC circuit. The time constant of this circuit lies between:
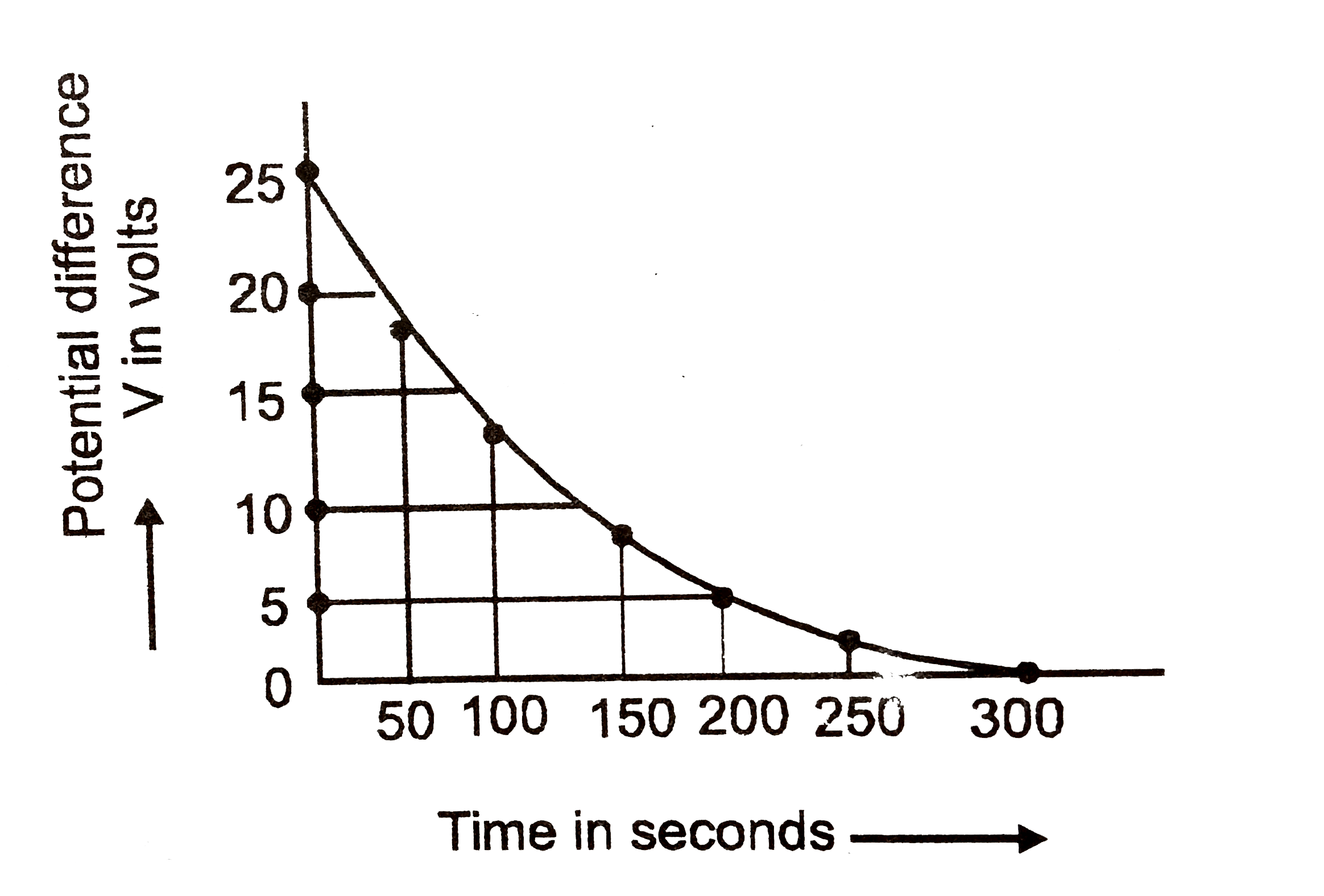
View SolutionShow that time constant (τ=RC) of R−C circuit has the dimensions of time.
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
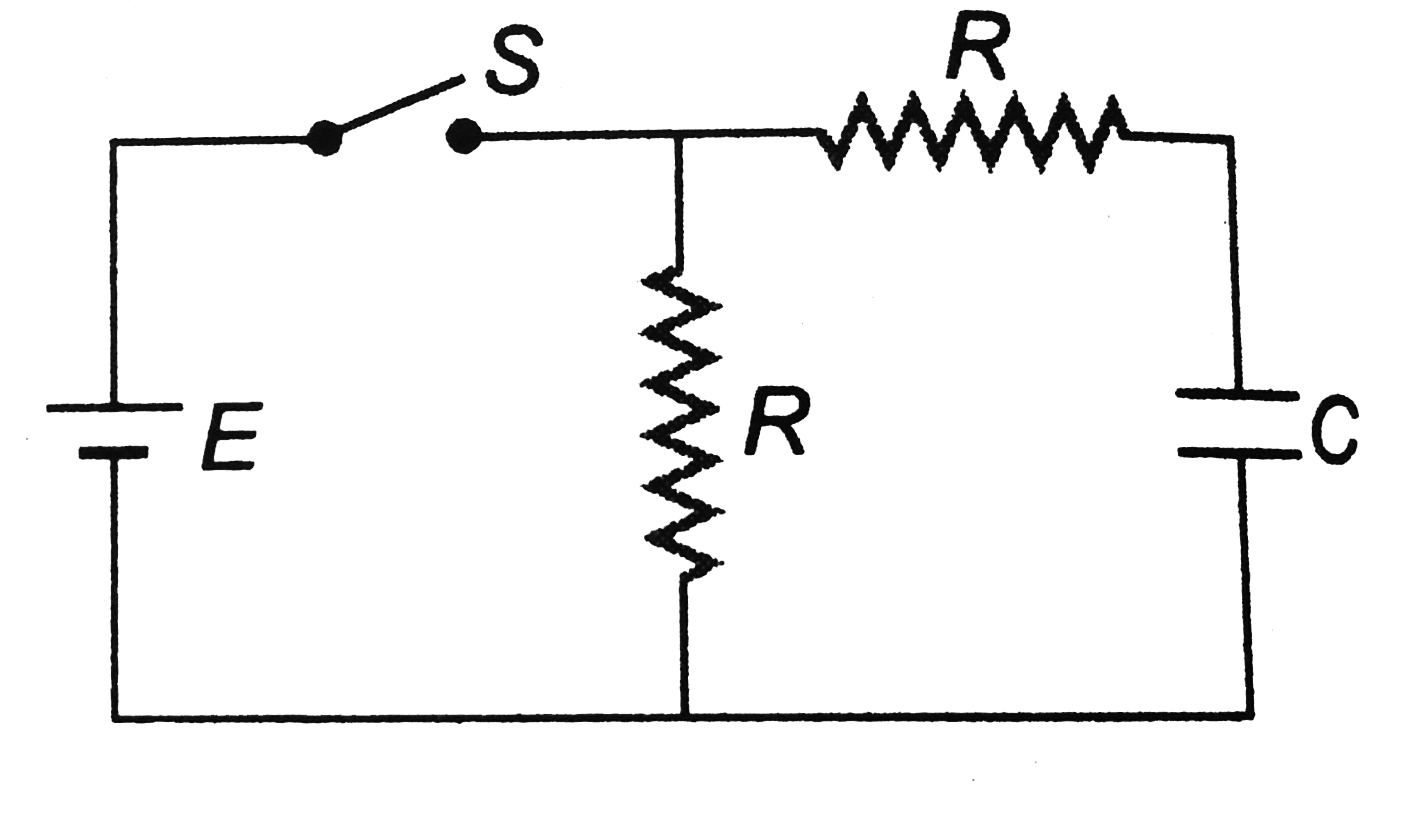
i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionIn the circuit shown in figure switch S is closed at time t=0, which statement is true after one time constant of L-R circuit?

View SolutionCombination of two identical capacitors, a resistor R and a dc voltage source of voltage 6V is used in an experiment on a (C−R) circuit. It is found that for a parallel combination of the capacitor the time in which the voltage of the fully charged combinatiomn reduces to half its original voltage is 10 second. For series combination the time needed for reducing teh voltage of the fully charged series combination by half is-
View SolutionTwo identical capacitors A and B are charged to the same potential V and are connected in two circuits at t = 0 as shown in figure. The charge of the capacitors at a time t = CR are respectively -
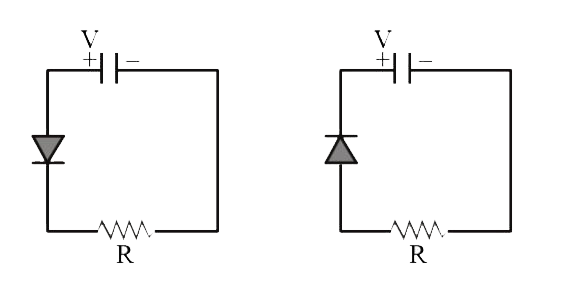
View Solution
