The centre and radius of a circle given by equation x=2+3cosθ,y=3sinθ−3 are Solution in Marathi
Step by step video & image solution for The centre and radius of a circle given by equation x =2 +3 cos theta, y =3 sin theta-3 are by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRYBOOK - BAL BHARTICHAPTER - TRIGONOMETRYEXERCISE - Practice set 6.1
17 Videos
- TRIGONOMETRYBOOK - BAL BHARTICHAPTER - TRIGONOMETRYEXERCISE - Practice set 6.2
6 Videos
- TRIGONOMETRYBOOK - BAL BHARTICHAPTER - TRIGONOMETRYEXERCISE - Problem set 6
18 Videos
- SIMILARITY BOOK - BAL BHARTICHAPTER - SIMILARITY EXERCISE - PROBLEM SET 1
12 Videos
Similar Questions
If sinθ=2029 , then find the value of cosθ.
View SolutionA person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45∘ . Find the height of the church.
View SolutionIf sinθ = 11/61 find the values of cosθ using trigonometric identity.
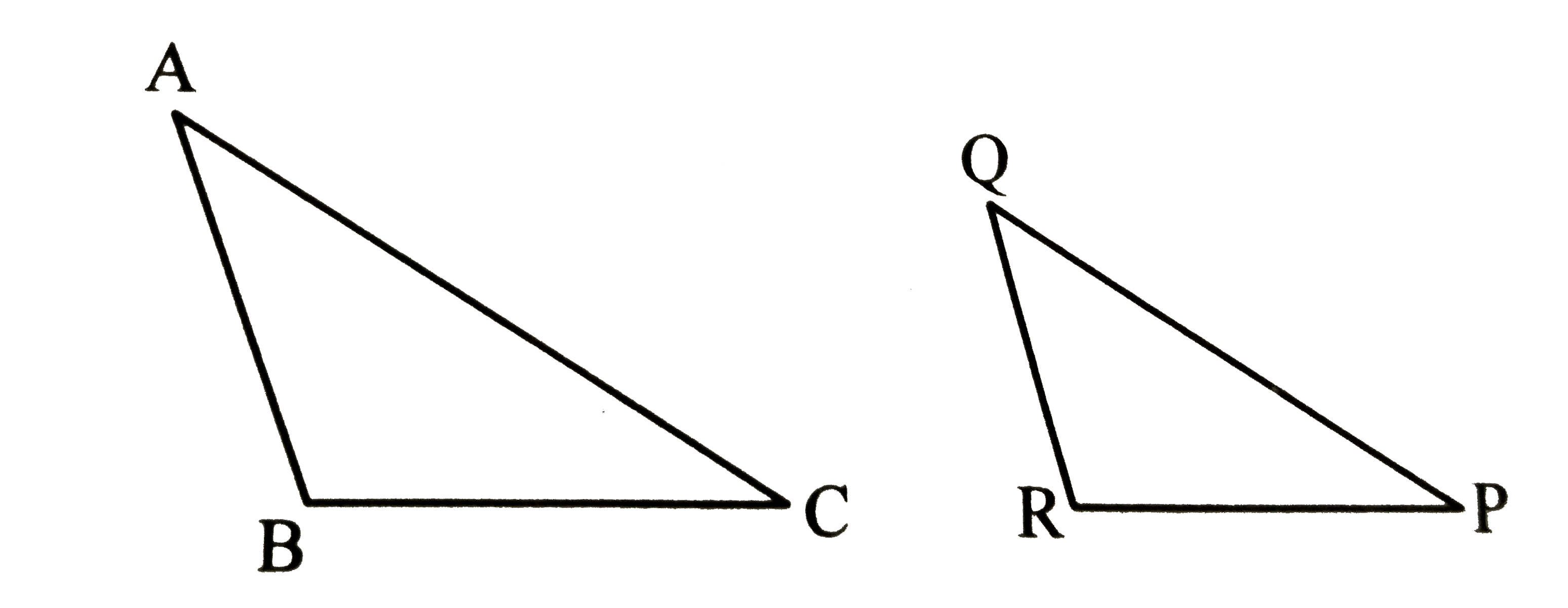
View SolutionIn ΔABCandΔPQR, in a one to one correspondence.
ABQR=BCPR=CAPQ, then
View SolutionFind the centre and radius of the circle whose parametric equation is x=−1+2cosθ,y=3+2sinθ.
View SolutionThe centre of the circle x=2+3cosθ,y=3sinθ−1, is
View SolutionThe equation of tangent to the curve given by
x=3cosθ,y=3sinθ,atθ=π4 is
View SolutionThe centre and radius of a circle given by equation x=2+3cosθ,y=3−3sinθ are
View SolutionIf x=−2+3cosθ,y=1+3sinθ then the locus of the point (x,y) is a circle with centre and radius
View Solutionसिद्ध कीजिए कि बिंदु (acos3θ,asin3θ) से होकर जाने वाली तथा सरल रेखा xsecθ+y cosecθ=a पर लम्ब रेखा का समीकरण xcosθ−ysinθ=acos2θ है |
View SolutionIfx=sinθ+cosθsin2θ and y=cosθ+sinθsin2θ,prove that (x+y)2/3+(x−y)2/3=2
View SolutionThe centre of the circle x=2+3cosθy=3sinθ−1 is ...
View SolutionIf x=2+3cosθ and y=1−3sinθ represent a circle then the centre and radius is
View SolutionIf x sin^3 theta + y cos ^3 theta = cos theta sin theta And x sin theta = y cos theta If so
View SolutionFind the centre and radius of the circle whose parametric equation is x=−1+2cosθ,y=3+2sinθ.
View SolutionEquation of the line passing through the point ( a cos^(3) theta , a sin^(3) theta ) and perpendicular to the line x sec theta + y cosec theta = a is x cos theta - y sin theta = cos 2 theta .
View Solution
