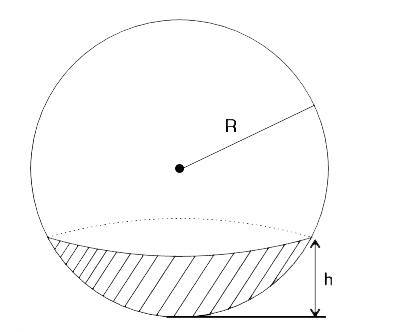
Find the volume of the spherical cap of height h cut of from a sphere of radius r

Text Solution

Verified by Experts

The correct Answer is: $(3 r - h)$

|

Updated on:21/07/2023

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

BOOK - NCERT TAMILCHAPTER - APPLICATIONS OF INTEGRATION EXERCISE - EXERCISE 9.8
5videos
APPLICATIONS OF INTEGRATION
BOOK - NCERT TAMILCHAPTER - APPLICATIONS OF INTEGRATION EXERCISE - EXERCISE 9.9
1videos
APPLICATIONS OF INTEGRATION
BOOK - NCERT TAMILCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUSEXERCISE - Exercise 7.10
20videos
APPLICATIONS OF DIFFERENTIAL CALCULUS
BOOK - NCERT TAMILCHAPTER - APPLICATIONS OF MATRICES AND DETERMINANTSEXERCISE - EXERCISE 1.8
25videos
APPLICATIONS OF MATRICES AND DETERMINANTS

Similar Questions

Knowledge Check

Question 1 - Select One
The volume of a spherical cap of height h cut off from a sphere of radius a is equal to :
A $\frac{π}{3} h^{2} (3 a - h)$
B $π (a - h) (2 a^{2} - h^{2} - a h)$
C $\frac{4 π}{3} h^{2}$
Dnone of the above
Question 2 - Select One
The volume of a spherical cap of height h cut off from a sphere of radius a is equal to :
A $\frac{π}{3} h^{2} (3 a - h)$
B $π (a - h) (2 a^{2} - h^{2} - a h)$
C $\frac{4 π}{3} h^{2}$
Dnone of the above

NCERT TAMIL-APPLICATIONS OF INTEGRATION -EXERCISE 9.10

Home
Ask Doubt
Profile