A mass 60 gram is suspended at 30 cm mark of a metre scale pivoted at midpoint. Then at what location, a weight of 40 gram can keep the metre scale horizontal ?
30 cm
70 cm
80 cm
95 cm
The correct Answer is:C
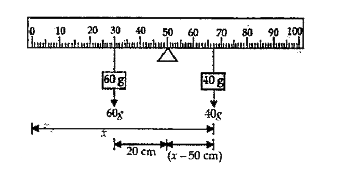
Let the distance of 40 g from the one end (ie, 0 cm) of the metre scale be x.
Distance of 60 g from midpoint=50 cm - 30 cm=20 cm
Distance of 40 g from midpoint = (x - 50) cm
Using principle of moments
Similar Questions
The working of a common balance or a physical balance is based on the 'Principle of moments . A metre scale of uniform density is balanced at the centre . If a mass of 2 kg is suspended at an adge of the scale then what mass should be suspended on other side at 1/4 th length of the scale to maintain the horizontal position of the scale ?
View SolutionA uniform metre scale 1 m long is suspended at 50 cm division. A known weight of 160 gwt is tied at 80 cm division and the scale is balanced by a weight of 240 gwt tied to the scale at a certain distance from the point of suspension on the opposite side. Calculate this distance.
View Solution
Knowledge Check
A metre scale is supported on a wedge at its centre of gravity. A body of weight w is suspended from the 15 cm mark and another weight of 30 gram suspended from 71 cm mark balances it the metre scale remains perfectly horizontal. What is the weight of the body? Neglect the weight of the centre scale.
A15 gram wtB18 gram wtC20 gram wtD25 gram wt.Find the weight of half meter scale balanced at 5 cm mark when a weight of 10 gf is suspended at one of its ends.
A2.5gfB100gfC0.2gfD50gfAn uniform metre scale of weight 50g is balanced at 60cm mark, when a weight of 15g is suspended at 10cm mark. Where must a weight 100g be suspended to balance metre scale.
A72.5cmB70cmC71.5cmD74.5cm
A uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end. Where should be a weight of 100 gf suspended to keep the rule horizontal?
View SolutionA uniform meter scale is kept in equilibrium when supported at the 60 cm mark and a mass weight of the scale is greater than, less than or equal to the weight of mass M.
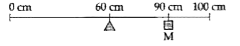
View SolutionA uniform metre rule is pivoted as its mid point. A weight of 50gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
View SolutionA heavy metallic scale of length 1 m has its centre of gravity at 50 cm division. It is suspended at a 30 cm mark. A load of 60gwt has to be tied at its zero cm make to keep it in equilibrium. Calculate the weight of the scale.
View SolutionA uniform metre scale of weight 20 gf is supported on a wedge placed at 60 cm mark. If a weight of 30 gf is suspended at 15 cm mark, where should a weight 200 gf be suspended in order to balance the metre scale?
View Solution
