Particles of masses 1g, 2g, 3g, ……. 100g re kept at the marks 1 cm, 2cm, 3cm,………. 100 cm, respectively on a metre scale. Find the moment of inertia of the system of particle about a perpendicular bisector of the metre scale.
The correct Answer is:B, C, D
To find the moment of inertia of a system of particles with masses from 1g to 100g placed at distances from 1 cm to 100 cm on a meter scale about the perpendicular bisector (which is at 50 cm), we can follow these steps:
1. Identify the Masses and Positions:
- The masses are m1=1g,m2=2g,…,m100=100g.
- The positions of these masses are x1=1cm,x2=2cm,…,x100=100cm.
2. Determine the Axis of Rotation:
- The perpendicular bisector of the meter scale is at x=50cm.
3. Calculate the Moment of Inertia:
- The moment of inertia I about an axis is given by:
I=∑mir2i
where ri is the distance from the axis of rotation to the mass mi.
4. Calculate for Left-Side Masses (1g to 49g):
- For masses m1 to m49:
- The distances from the axis (50 cm) are:
- r1=50−1=49cm
- r2=50−2=48cm
- ...
- r49=50−49=1cm
- Thus, the moment of inertia for the left-side masses is:
IL=49∑i=1mi(50−i)2
5. Calculate for Right-Side Masses (51g to 100g):
- For masses m51 to m100:
- The distances from the axis (50 cm) are:
- r51=51−50=1cm
- r52=52−50=2cm
- ...
- r100=100−50=50cm
- Thus, the moment of inertia for the right-side masses is:
IR=100∑i=51mi(i−50)2
6. Combine Both Moments of Inertia:
- The total moment of inertia is:
I=IL+IR
7. Calculate Each Sum:
- For IL:
IL=10−449∑i=1i(49−i+1)2
- For IR:
IR=10−4100∑i=51i(i−50)2
8. Final Calculation:
- After calculating both sums, combine them to find I.
Final Result:
After performing the calculations, the moment of inertia about the perpendicular bisector is found to be approximately 0.43kg m2.
---
- The masses are m1=1g,m2=2g,…,m100=100g.
- The positions of these masses are x1=1cm,x2=2cm,…,x100=100cm.
- The perpendicular bisector of the meter scale is at x=50cm.
- The moment of inertia I about an axis is given by:
I=∑mir2i
where ri is the distance from the axis of rotation to the mass mi.
- For masses m1 to m49:
- The distances from the axis (50 cm) are:
- r1=50−1=49cm
- r2=50−2=48cm
- ...
- r49=50−49=1cm
- Thus, the moment of inertia for the left-side masses is:
IL=49∑i=1mi(50−i)2
- For masses m51 to m100:
- The distances from the axis (50 cm) are:
- r51=51−50=1cm
- r52=52−50=2cm
- ...
- r100=100−50=50cm
- Thus, the moment of inertia for the right-side masses is:
IR=100∑i=51mi(i−50)2
- The total moment of inertia is:
I=IL+IR
- For IL:
IL=10−449∑i=1i(49−i+1)2
- For IR:
IR=10−4100∑i=51i(i−50)2
- After calculating both sums, combine them to find I.
After performing the calculations, the moment of inertia about the perpendicular bisector is found to be approximately 0.43kg m2.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Particles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular besector of the metre scale.
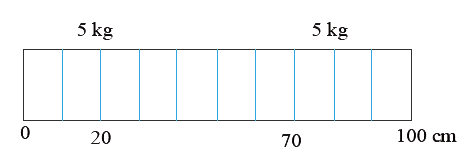
View SolutionTwo masses of 3kg and 5kg are placed at 20 cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passign through 100cm mark and perpendicular to the meter scale is
View Solution
Knowledge Check
Two masses of 500 gram and 600 grams are attached to the 10 cm and 80 cm marks respectively of a light metre scale. The moment of inertia of this system about an axis passing through the centre of the scale will be
A0.134 kg-m2B2 kg-m2C0.56 kg-m2D4.5 kg-m2Particles of masses 1g, 2g, 3g, ……. 100g re kept at the marks 1 cm, 2cm, 3cm,………. 100 cm, respectively on a metre scale. Find the moment of inertia of the system of particle about a perpendicular bisector of the metre scale.
A55 cm markB60 cm markC66 cm markD72 cm markThree particles of masses 1gm,2gm&3gm are at 1cm,2cm&3cm from the axis of rotation respectively then the moment of inertia of the system & radius of gyration of the system respectively are …. gmcm2 and ….. cm
A63,2.449B60,4.5C36,4.449D36,2.449
Three particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm−cm(2)) about (a) x-axis
(b). Y-axis
(c). Z-axis.
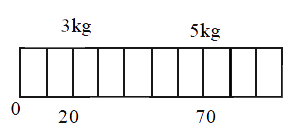
View SolutionTwo masses of 3kg and 5kg are placed at 20cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passing through 100 cm mark and perpendicular to the meter scale is
View SolutionThree particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View Solution10gm,30gm and 60gm are at 20cm,40cm and 80cm on light metre scale.The position of the centre of mass of the system is (in )
View SolutionWeights of 1g, 2g,...., 100g are suspended from the 1-cm, 2-cm,......, 100-cm marks respectively of a light meter scale. Where should it be supported for the system to be in equilibrium ?
View Solution
