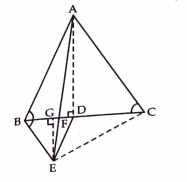
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(BFE) = 2ar(FED)Solution in Punjabi
Step by step video & image solution for ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(BFE) = 2ar(FED) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SWAN PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - OBJECTIVE TYPE QUESTIONS20videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - EXERCISE 9.321videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - CIRCLESEXERCISE - Objective Type Questions (Fill in the Blanks :)10videos
CIRCLES
Similar Questions
State whether the following statements are true (T) or false (F) :
If A and B are two congruent figures then their areas will be equal .02:11View SolutionIn Fig ., E is any point on median AD of a ΔABC . Show that ar (ABE = ar (ACE) .
 02:45View Solution
02:45View Solution............... is the longest chord of the circle.
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionThe inequation represented by the graph given below is :
03:02View SolutionThe inequation that best describes the graph given below is _________
03:10View SolutionThe inequation that best describes the following graph is _________
03:07View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt02:36View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt03:17View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
01:46View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/4 ar( Delta ABC)
06:45View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/2 ar( Delta BAE)
02:37View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta ABC) = 2 ar( Delta BEC)
03:21View Solution

