In Fig ., ABC and BDE are two equilateral triangles such that D is the mid -point of BC .If AE intersects BC at F , show that
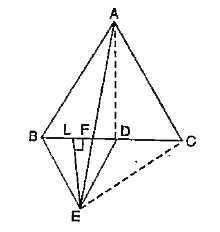
ar(ABC)=2ar(BEC)Solution in Punjabi
Step by step video & image solution for In Fig ., ABC and BDE are two equilateral triangles such that D is the mid -point of BC .If AE intersects BC at F , show that ar (ABC)=2ar(BEC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SWAN PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - OBJECTIVE TYPE QUESTIONS20videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - EXERCISE 9.321videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - CIRCLESEXERCISE - Objective Type Questions (Fill in the Blanks :)10videos
CIRCLES
Similar Questions
State whether the following statements are true (T) or false (F) :
If A and B are two congruent figures then their areas will be equal .02:11View SolutionIn Fig ., E is any point on median AD of a ΔABC . Show that ar (ABE = ar (ACE) .
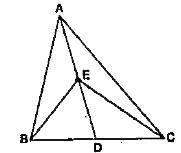 04:23View Solution
04:23View Solution............... is the longest chord of the circle.
02:17View SolutionDetermine the point of symmetry of a regular hexagon.
05:41View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionThe inequation represented by the graph given below is :
03:10View SolutionThe inequation that best describes the graph given below is _________
06:30View SolutionThe inequation that best describes the following graph is _________
03:07View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt02:36View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
03:17View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
01:46View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/4 ar( Delta ABC)
06:45View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/2 ar( Delta BAE)
02:37View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta ABC) = 2 ar( Delta BEC)
03:21View Solution

