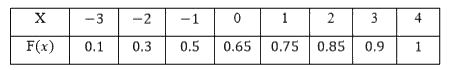Verify which of the following is p.d.f. of r.v.X :
f(x)=isx for 0≤x≤π2
Text Solution
The correct Answer is:p.d.f
|
Similar Questions
Knowledge Check
The function f(x)=cosx,0≤x≤π is
AdecreasingBincreasingCneither increasing nor decreasingDincreasing for 0≤x≤πIf the p.d.f. of a r.v. X is
f(x)=K.e−θx,θ>0,0≤x<∞
=0 , otherwise
Then, K =Aθ3Bθ2CθD2θSuppose f:[−2,2]→R is defined by f(x)={−1 for −2≤x≤0x−1 for 0≤x≤2 , then {x∈[−2,2]:x≤0andf(|x|)=x}=
A{−1}B{0}C{−1/2}Dϕ
Find the area bounded by the following curve :
(i) f(x)=sinx,g(x)=sin2x,0≤x≤2π
(ii) f(x)=sinx,g(x)=sin4x,0≤x≤2π
View SolutionFind the area bounded by the following curve :
(i) f(x)=sinx,g(x)=sin2x,0≤x≤2π
(ii) f(x)=sinx,g(x)=sin4x,0≤x≤2π
View SolutionExpress each of the following sts as an interval :
(i)A={x:x∈R,−4,<x<0}
(ii)B={x:x∈R,0≤x<3}
(iii)C={x:x∈R,2<x≤6}
(iv)D={x:x∈R,−5≤x≤2}
(v)E={x:x∈R,−3≤x<2)
(vi)F={x:x∈R,−2,≤x<0}
View SolutionSuppose f:[−2,2]→R is defined by f(x)={−1 for −2≤x≤0x−1 for 0≤x≤2 , then {x∈[−2,2]:x≤0andf(|x|)=x}=
View SolutionWrite the interval for which the function f(x)=cosx,0≤x≤2π is decreasing
View Solution