ABC is a triangle where BC = 2AB, ∠C=30∘ and ∠A=90∘. The magnitude of the side AC is:
2BC3
3BC4
BC√3
√3BC2
Step by step video & image solution for ABC is a triangle where BC = 2AB, angleC = 30^(@) and angleA = 90^(@). The magnitude of the side AC is: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
ABC is a triangle, where BC = 2AB , ∠B = 30∘ and ∠A = 90∘. The magnitude of the side AC is
A2BC3B3BC4CBC√3D√3BC2In △ABC , AB=BC , ∠B=40∘ Then ∠A is equal to
A70∘B40∘C140∘D100∘ABC is a right triangle with ∠B=90∘ and AC - AB = 1. If BC=√n then AB is
An+12Bn−12Cn2Dn−32
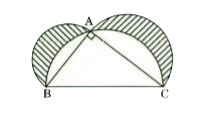
In the figure given below, ABC is a right-angled triangle where ∠A=90∘, AB = p cm and AC = q cm. On the three sides as diameters semicircles are drawn as shown in the figure. The area of the shaded portion, in square cm, is
View SolutionABC is a right angled triangle in which ∠B=90∘andAB=BC. Find ∠Aand∠C.
View SolutionIn ΔABC,∠A=50∘,∠B=30∘and∠C=100∘ What are the angles of the triangle formed by joining the midpoints of the sides of this triangle?
View SolutionIn a △ABC,∠B=35∘ and ∠C=55∘.Write of the following is true
AC2=AB2+BC2
AB2=BC2+AC2
BC2=AB2+AC2

View SolutionIn ΔABC, if ∠A=60∘,∠B=50∘,and∠C=70∘, then find the longest side of the triangle ABC.
View Solution
