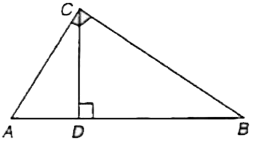
In a right-angled triangle ABC, and CD is perpendicular to AB. If AB x CD = CA x CB, then is equal to:
if
To solve the problem, we need to analyze the given right-angled triangle ABC, where angle C is 90 degrees, and CD is perpendicular to AB. We are given the relationship AB×CD=CA×CB and need to find the value of 1CD2.
1. Understand the Triangle Setup:
- We have a right-angled triangle ABC with ∠C=90∘.
- CD is drawn perpendicular to AB.
2. Use the Given Relationship:
- From the problem, we know that:
AB×CD=CA×CB
3. Rearranging the Equation:
- We can rearrange the equation to isolate CD:
CD=CA×CBAB
4. Finding 1CD2:
- We need to find 1CD2:
1CD2=AB2(CA×CB)2
5. Applying Pythagorean Theorem:
- In triangle ABC, by the Pythagorean theorem:
AB2=AC2+BC2
6. Substituting AB2:
- Substitute AB2 in the equation:
1CD2=AC2+BC2(CA×CB)2
7. Separating the Terms:
- We can separate the fractions:
1CD2=AC2(CA×CB)2+BC2(CA×CB)2
8. Simplifying Each Fraction:
- This simplifies to:
1CD2=1CB2+1CA2
9. Final Result:
- Therefore, we conclude:
1CD2=1BC2+1CA2
Conclusion:
The final answer is:
1CD2=1BC2+1CA2
- We have a right-angled triangle ABC with ∠C=90∘.
- CD is drawn perpendicular to AB.
- From the problem, we know that:
AB×CD=CA×CB
- We can rearrange the equation to isolate CD:
CD=CA×CBAB
- We need to find 1CD2:
1CD2=AB2(CA×CB)2
- In triangle ABC, by the Pythagorean theorem:
AB2=AC2+BC2
- Substitute AB2 in the equation:
1CD2=AC2+BC2(CA×CB)2
- We can separate the fractions:
1CD2=AC2(CA×CB)2+BC2(CA×CB)2
- This simplifies to:
1CD2=1CB2+1CA2
- Therefore, we conclude:
1CD2=1BC2+1CA2
The final answer is:
1CD2=1BC2+1CA2
Similar Questions
Knowledge Check
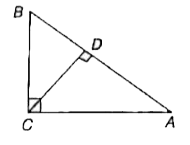
In a right angled ΔABC,∠C=90∘andCD is the perpendicular on hypotenuse AB if BC = 15 cm and AC=20cm then CD is equal to :
 A18 cmB12 cmC17.5 cmDcan't be determined
A18 cmB12 cmC17.5 cmDcan't be determinedIn ΔABC,∠C=90∘ and CD is perpendicular to AB at D. If ADBD=√k, then ACBC=?
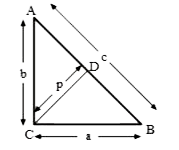
Aa)kBb)√kCc)1√kDd)4√kIn a right angled ΔABC,∠C=90∘andCD is the perpendicular on the hypotenuse AB,AB=c,BC=a,AC=bandCD=p, then :
 Apq=pbB1p2+1b2=1a2Cp2=b2+c2D1p2=1a2+1b2
Apq=pbB1p2+1b2=1a2Cp2=b2+c2D1p2=1a2+1b2
ΔABC is an isosceles triangle. AB = AC and BD is perpendicular on AC from vertex B, then BD2−CD2 is equal to-
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View SolutionIn a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
View SolutionIn a right triangle ABC, in which ∠C=90∘amdCD⊥AB. If BC =a, CA=b, AB=c and CD=p, then
View SolutionIn ΔABC,IfAD⊥BC, then AB2+CD2 is equal to
View Solution
