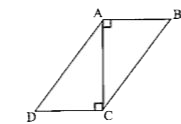
ABCD is a quadrilateral such that AD=DC=CA=20 units, BC= 12 units and ∠ABC=90∘. What is the approximate area of the quadrilateral ABCD
269 sq units
300 sq units
325 sq units
349 sq units
To find the area of quadrilateral ABCD, we can break it down into two parts: triangle ACD and triangle ABC.
1. Identify the triangles in the quadrilateral:
- Quadrilateral ABCD consists of triangle ACD and triangle ABC.
- Given that AD = DC = CA = 20 units and BC = 12 units, we can analyze the triangles.
2. Calculate the area of triangle ACD:
- Triangle ACD is an equilateral triangle since all sides are equal (AD = DC = CA).
- The formula for the area of an equilateral triangle is:
Area=√34a2
where a is the length of a side.
- Here, a=20 units.
- Thus, the area of triangle ACD is:
AreaACD=√34×202=√34×400=100√3≈173.2 square units
3. Calculate the length of AB using the Pythagorean theorem:
- In triangle ABC, angle ABC is 90 degrees.
- We can use the Pythagorean theorem:
AC2=AB2+BC2
- Substituting the known values:
202=AB2+122
400=AB2+144
AB2=400−144=256
AB=√256=16 units
4. Calculate the area of triangle ABC:
- The area of triangle ABC can be calculated using the formula:
Area=12×base×height
- Here, we can take BC as the base (12 units) and AB as the height (16 units):
AreaABC=12×12×16=96 square units
5. Calculate the total area of quadrilateral ABCD:
- The total area of quadrilateral ABCD is the sum of the areas of triangles ACD and ABC:
AreaABCD=AreaACD+AreaABC=100√3+96≈173.2+96=269.2 square units
Final Answer:
The approximate area of quadrilateral ABCD is 269.2 square units.
- Quadrilateral ABCD consists of triangle ACD and triangle ABC.
- Given that AD = DC = CA = 20 units and BC = 12 units, we can analyze the triangles.
- Triangle ACD is an equilateral triangle since all sides are equal (AD = DC = CA).
- The formula for the area of an equilateral triangle is:
Area=√34a2
where a is the length of a side.
- Here, a=20 units.
- Thus, the area of triangle ACD is:
AreaACD=√34×202=√34×400=100√3≈173.2 square units
- In triangle ABC, angle ABC is 90 degrees.
- We can use the Pythagorean theorem:
AC2=AB2+BC2
- Substituting the known values:
202=AB2+122
400=AB2+144
AB2=400−144=256
AB=√256=16 units
- The area of triangle ABC can be calculated using the formula:
Area=12×base×height
- Here, we can take BC as the base (12 units) and AB as the height (16 units):
AreaABC=12×12×16=96 square units
- The total area of quadrilateral ABCD is the sum of the areas of triangles ACD and ABC:
AreaABCD=AreaACD+AreaABC=100√3+96≈173.2+96=269.2 square units
The approximate area of quadrilateral ABCD is 269.2 square units.
Similar Questions
Knowledge Check
In the adjoining figure, the area of quadrilateral ABCD is
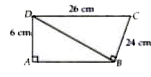 A148 cm2B144cm2C120 cm2D122 cm2
A148 cm2B144cm2C120 cm2D122 cm2
ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the area of quadrilateral ABCD ?
View SolutionIn Figure, ABCD is a quadrilateral and BE∣AC and also BE meets DC produced at E. Show that area of ADE is equal to the area of the quadrilateral ABCD

View SolutionThe given figure shows a quadrilateral ABCD.
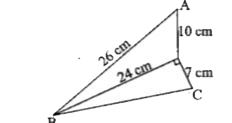
What is the area of quadrilateral ABCD?
View SolutionIn Fig. 9.22, ABCD is a quadrilateral and BE ∣∣ ACand also BE meets DC produced at E. Show that area of ΔADEis equal to the area of the quadrilateral ABCD.
View SolutionIn the quadrilateral ABCD,AC=8√3cm, angle CAB=30∘ angle ADC=60∘ angle ABC = angle ACD=90∘. Find the area of the quadrilateral ABCD.
View SolutionIn Figure, ABCD is a quadrilateral and BE⊥AC and also BE meets DC produced at E , Show that area of ADE is equal to the area of the quadrilateral ABCD.
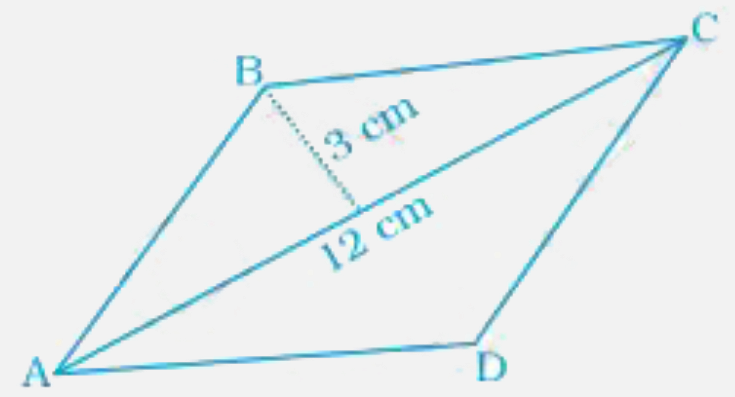
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View Solution