ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the area of quadrilateral ABCD ?
300cm2
306cm2
312cm2
316cm2
To find the area of quadrilateral ABCD, we can divide it into two triangles: triangle ABC and triangle ADC.
1. Identify the triangles:
- Triangle ABC is a right triangle with AB = 9 cm and BC = 40 cm.
- Triangle ADC has sides AD = 15 cm, CD = 28 cm, and AC (which we will calculate).
2. Calculate the length of AC using the Pythagorean theorem:
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AC2=AB2+BC2
AC2=92+402=81+1600=1681
AC=√1681=41 cm
3. Calculate the area of triangle ABC:
- The area of a right triangle can be calculated using the formula:
Area=12×Base×Height
- Here, Base = AB = 9 cm and Height = BC = 40 cm:
AreaABC=12×9×40=3602=180 cm2
4. Calculate the semi-perimeter of triangle ADC:
- The semi-perimeter s is given by:
s=AD+CD+AC2=15+28+412=842=42 cm
5. Use Heron's formula to find the area of triangle ADC:
- Heron's formula states:
Area=√s(s−a)(s−b)(s−c)
- Here, let a=AD=15, b=CD=28, c=AC=41:
AreaADC=√42(42−15)(42−28)(42−41)
=√42×27×14×1
=√42×378=√15876
- Calculating √15876:
=126 cm2
6. Calculate the total area of quadrilateral ABCD:
- The total area is the sum of the areas of triangles ABC and ADC:
AreaABCD=AreaABC+AreaADC=180+126=306 cm2
Final Answer:
The area of quadrilateral ABCD is 306 cm².
- Triangle ABC is a right triangle with AB = 9 cm and BC = 40 cm.
- Triangle ADC has sides AD = 15 cm, CD = 28 cm, and AC (which we will calculate).
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AC2=AB2+BC2
AC2=92+402=81+1600=1681
AC=√1681=41 cm
- The area of a right triangle can be calculated using the formula:
Area=12×Base×Height
- Here, Base = AB = 9 cm and Height = BC = 40 cm:
AreaABC=12×9×40=3602=180 cm2
- The semi-perimeter s is given by:
s=AD+CD+AC2=15+28+412=842=42 cm
- Heron's formula states:
Area=√s(s−a)(s−b)(s−c)
- Here, let a=AD=15, b=CD=28, c=AC=41:
AreaADC=√42(42−15)(42−28)(42−41)
=√42×27×14×1
=√42×378=√15876
- Calculating √15876:
=126 cm2
- The total area is the sum of the areas of triangles ABC and ADC:
AreaABCD=AreaABC+AreaADC=180+126=306 cm2
The area of quadrilateral ABCD is 306 cm².
Similar Questions
ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the difference between perimeter of triangle ABC and perimeter of triangle ADC ?
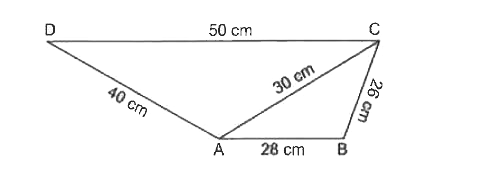
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
View Solution
Knowledge Check
ABCD is a quadrilateral in which AB = 5 cm, CD = 8 cm and the sum of angle A and angle D is 180°. What is the name of this quadrilateral?
AParallelogramBTrapeziumCRhombusDCan not be determinedABCD is a cyclic quadrilateral in which AB = 15 cm, BC = 12 cm and CD = 10 cm. If AC bisects BD, then what is the measure of AD?
A15 cmB13.5 cmC18 cmD20 cmABCD is a cyclic quadrilateral in which AB= 16.5 cm, BC = x cm, CD = 11 cm, AD= 19.8 cm and BD is bisected by AC at O. What is the value of x?/
ABCD एक चक्रीय चतुर्भुज है जिसमें AB = 16.5 सेमी, BC = x सेमी, CD = 11 सेमी, AD = 19.8 सेमी है तथा BD को AC के द्वारा O पर समद्विभाजित किया जाता है | x का मान क्या है ?A13.8 cmB12.4 cmC12.8 cmD13.2 cm
Construct a quadrilateral ABCD with AB = 4 cm, BC = 2.8 cm, CD = 4 cm, ∠B=75∘and∠C=105∘
View SolutionIn a quadrilateral ABCD , AB = 5 cm , BC = 37 cm , CD = 35 cm , BD = 12 cm , and AD = 13 cm . Find its area .
View SolutionConstruct a quadrilateral ABCD in which AB=3.8cm, BC=5cm,CD=5cm, DA=5.5cm and AC=8cm.
View SolutionThe base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
View SolutionA park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
View Solution