ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC ?
15
30
25
10
The correct Answer is:A
To solve for the value of angle BEC in the given configuration of square ABCD and equilateral triangle CDE, we can follow these steps:
1. Identify the Angles in the Equilateral Triangle:
- Since CDE is an equilateral triangle, all its angles are equal to 60 degrees. Therefore, angle DCE = angle CED = angle CDE = 60 degrees.
Hint: Remember that in an equilateral triangle, all sides and angles are equal.
2. Identify the Angles in the Square:
- In square ABCD, all angles are right angles (90 degrees). Therefore, angle ABC = 90 degrees.
Hint: A square has four right angles, each measuring 90 degrees.
3. Determine Angle BEC:
- In triangle BEC, we know angle BEC is the angle we want to find, angle CBE is the angle formed by line BC and line BE, and angle CEB is the angle formed by line CE and line BE.
- From the previous steps, we know:
- Angle CBE = angle ABC + angle DCE = 90 degrees + 60 degrees = 150 degrees.
Hint: The angle CBE is the sum of the right angle from the square and the angle from the equilateral triangle.
4. Use the Triangle Angle Sum Property:
- The sum of the angles in triangle BEC is 180 degrees. Therefore:
Angle BEC+Angle CBE+Angle CEB=180 degrees
- We already know angle CBE = 150 degrees and angle CEB = 60 degrees (since it is also part of the equilateral triangle).
- Plugging in the values:
Angle BEC+150+60=180
Angle BEC+210=180
Angle BEC=180−210=−30 degrees
- Since angles cannot be negative, we must have made an error in our assumptions about angle CEB. Let's correct that.
5. Correct Calculation of Angle CEB:
- Since angle CEB is actually the angle opposite to angle CBE, we can use the fact that angle CEB = 30 degrees (as it is the remaining angle in the triangle).
- Thus, we have:
Angle BEC+150+30=180
Angle BEC+180=180
Angle BEC=0 degrees
- This indicates that angles were miscalculated. Let's recalculate angle BEC directly.
6. Final Calculation:
- Since angle BEC is actually the external angle at point E, we can use:
Angle BEC=180−Angle CBE=180−150=30 degrees
Conclusion:
The value of angle BEC is 30 degrees.
- Since CDE is an equilateral triangle, all its angles are equal to 60 degrees. Therefore, angle DCE = angle CED = angle CDE = 60 degrees.
- In square ABCD, all angles are right angles (90 degrees). Therefore, angle ABC = 90 degrees.
- In triangle BEC, we know angle BEC is the angle we want to find, angle CBE is the angle formed by line BC and line BE, and angle CEB is the angle formed by line CE and line BE.
- From the previous steps, we know:
- Angle CBE = angle ABC + angle DCE = 90 degrees + 60 degrees = 150 degrees.
- The sum of the angles in triangle BEC is 180 degrees. Therefore:
Angle BEC+Angle CBE+Angle CEB=180 degrees
- We already know angle CBE = 150 degrees and angle CEB = 60 degrees (since it is also part of the equilateral triangle).
- Plugging in the values:
Angle BEC+150+60=180
Angle BEC+210=180
Angle BEC=180−210=−30 degrees
- Since angles cannot be negative, we must have made an error in our assumptions about angle CEB. Let's correct that.
- Since angle CEB is actually the angle opposite to angle CBE, we can use the fact that angle CEB = 30 degrees (as it is the remaining angle in the triangle).
- Thus, we have:
Angle BEC+150+30=180
Angle BEC+180=180
Angle BEC=0 degrees
- This indicates that angles were miscalculated. Let's recalculate angle BEC directly.
- Since angle BEC is actually the external angle at point E, we can use:
Angle BEC=180−Angle CBE=180−150=30 degrees
The value of angle BEC is 30 degrees.
Similar Questions
In the given figure, ABCD is a square, BCXYZ is a regular pentagon and ABE is an equilateral triangle. What is the value (in degrees) of ∠EBZ?
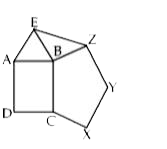
View SolutionIn the given figure , ABCD is a square BCXYZ is a regular pentagon and ABE is an equilateral triangle . What is the value (in degrees) of ∠EBZ ?
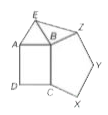
View Solution
Knowledge Check
ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC?
A15B30C25D10ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
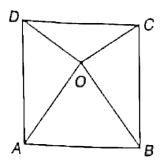 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determined
ABCD is square . BCE is equilateral Δ outside . Find ∠DEC
View SolutionABCD is a square. BEC is an equilateral triangle inside the square. If CE & BD intersects at O. Find ∠BOC=?
View SolutionIn the given figure, PQRS is a square and SRT is an equliateral triangle. What is the value (in digrees) of ∠SOR ?
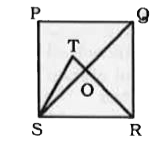
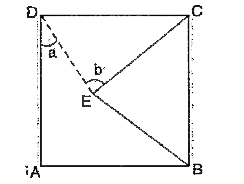
View SolutionABCD is a square and BCE is an equilateral triangle. Find the value of a,b and reflex ∠BED.
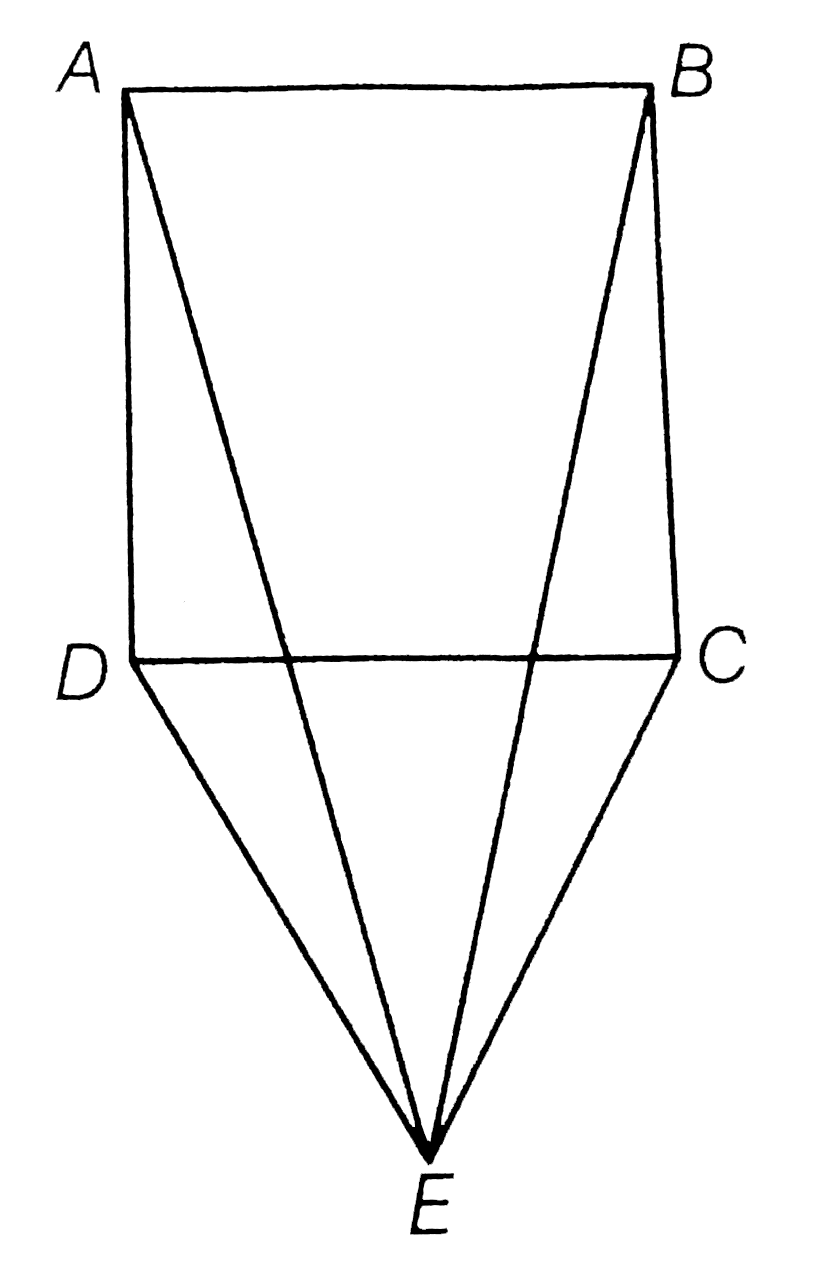
View SolutionIn the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
View Solution
