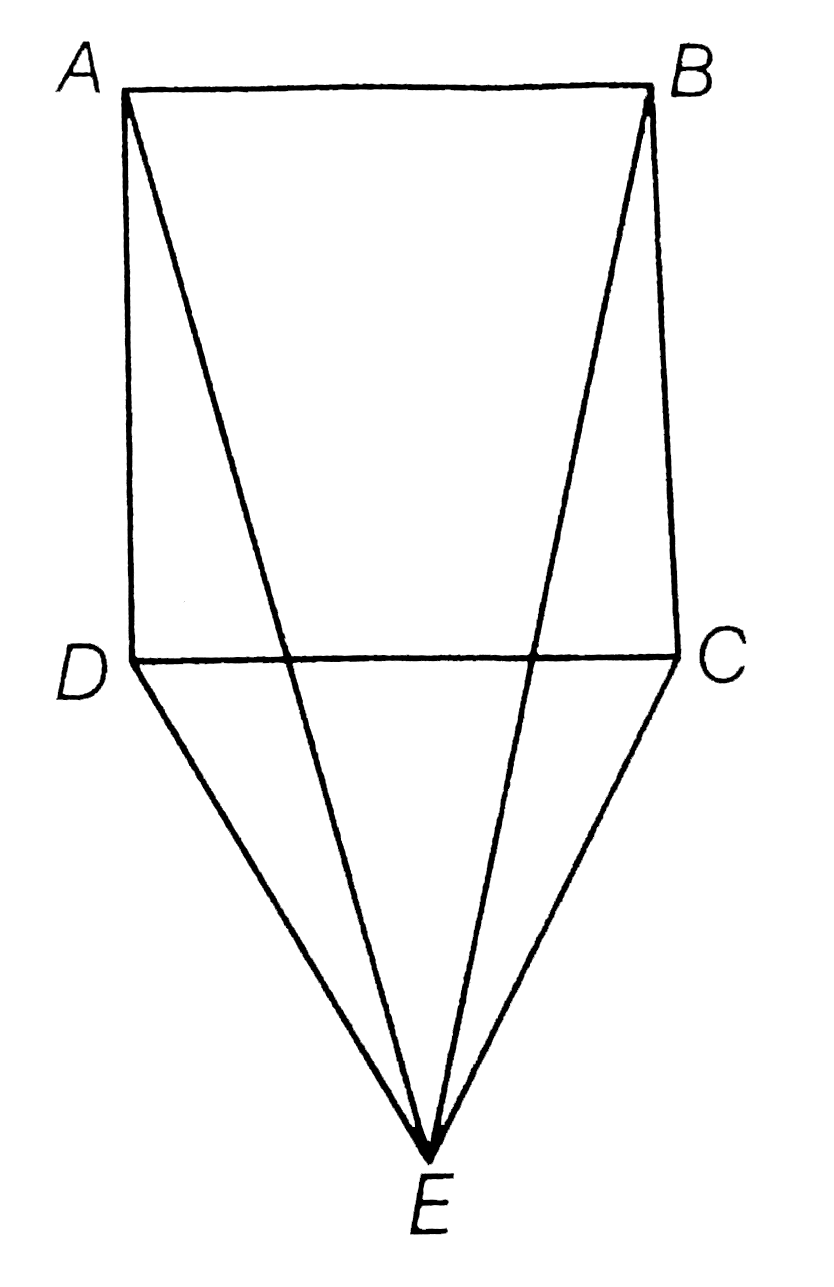
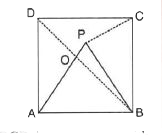
In the given figure, is an equilateral triangle triangle formed on a side of a square . Show that
Video Solution
Text Solution
Given in figure is an equilateral triangle formed on a side CD of a square ABCD.
To show
Proof in
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS21videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS8videos
VOLUME AND SURFACE AREA
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3
In the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
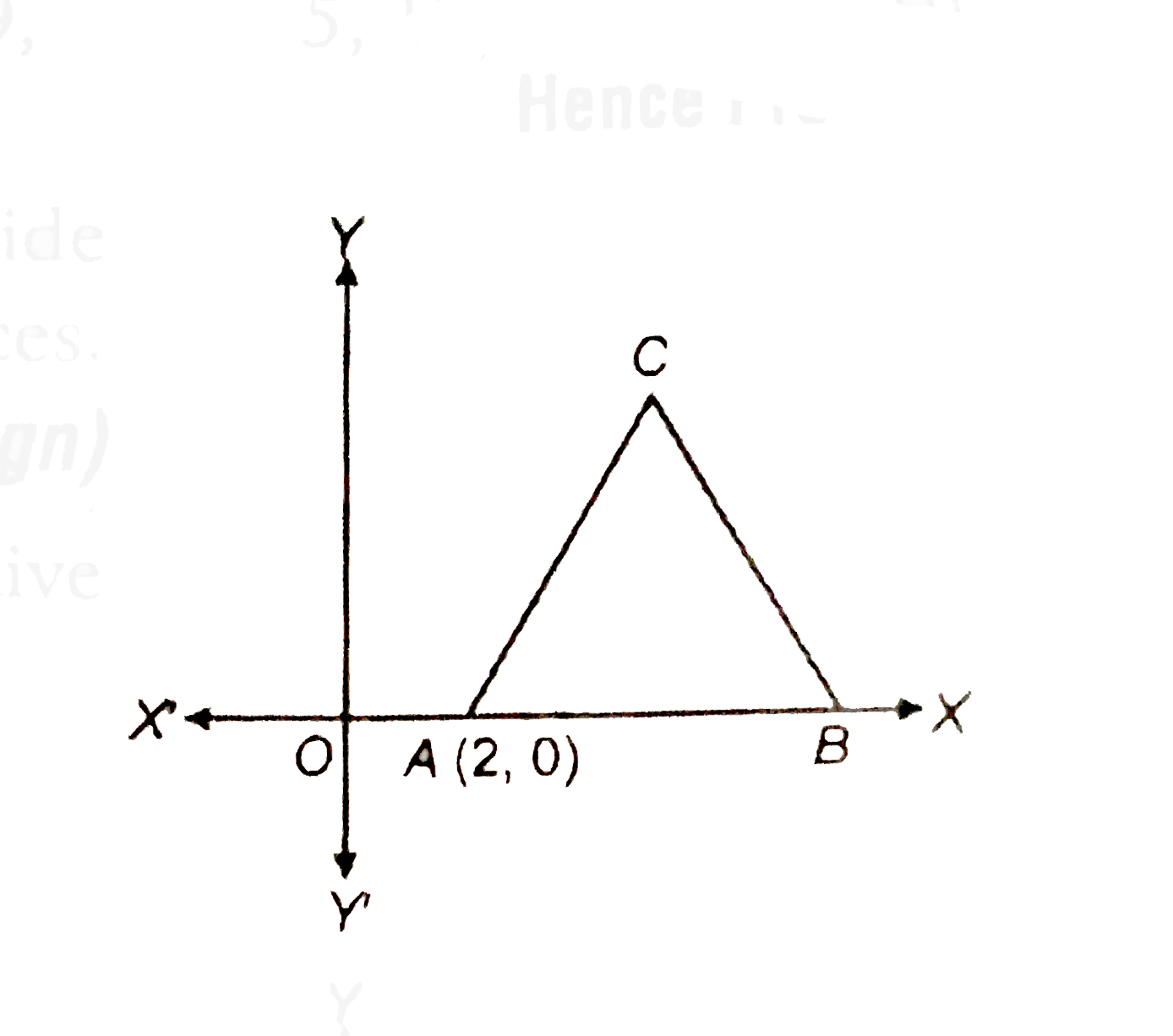 View Solution
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
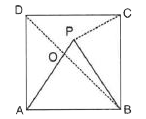
∠PCDView SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
∠BPCView SolutionConstruct an equilateral triangle of sides 6 cm each.
View SolutionFind the perimeter of an equilateral triangle with side 9cm.
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
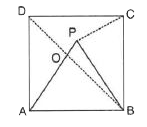
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
∠AOBView Solution

