The value of F so that the block will remain in equilibrium is:

20 N
30 N
40 N
none
The correct Answer is:d

As the body is in equilibrium
Along horizontal direction
2Fcos45∘=Fcos60∘+10
⇒F=202√2−1N
Topper's Solved these Questions
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - MANDATORY EXERCISE
8 Videos
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - CONSOLIDATED EXERCISE
3 Videos
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - MANDATORY EXERCISE SET II
9 Videos
- SOUNDBOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
8 Videos
Similar Questions
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View Solution
Knowledge Check
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is
 AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−Qcosθ
AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−QcosθWhat should be the value of F so that block of mass 1 kg remains in equilibrium. The co-efficient of friction between 1 kg and 4 kg block is 0.5 and except it all surfaces are smooth :-
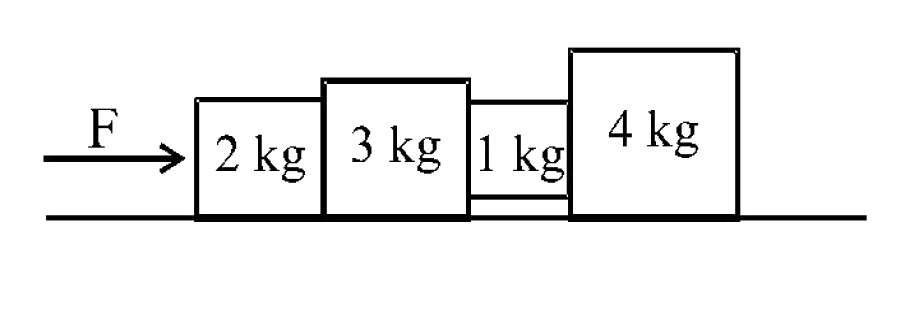 A220NB170NC135ND50N
A220NB170NC135ND50NIn the system shown in Fig the friction coefficient between ground and bigger block is μ There is no friction between both the block .The string connecting both the block is light all three pulley are light and frictionless Then the minimum limiting value of μ so that the system remain in equilibrium , is
 A12B13C23D32
A12B13C23D32
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

View SolutionIn the system shown in Fig the friction coefficient between ground and bigger block is μ There is no friction between both the block .The string connecting both the block is light all three pulley are light and frictionless Then the minimum limiting value of μ so that the system remain in equilibrium , is

View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
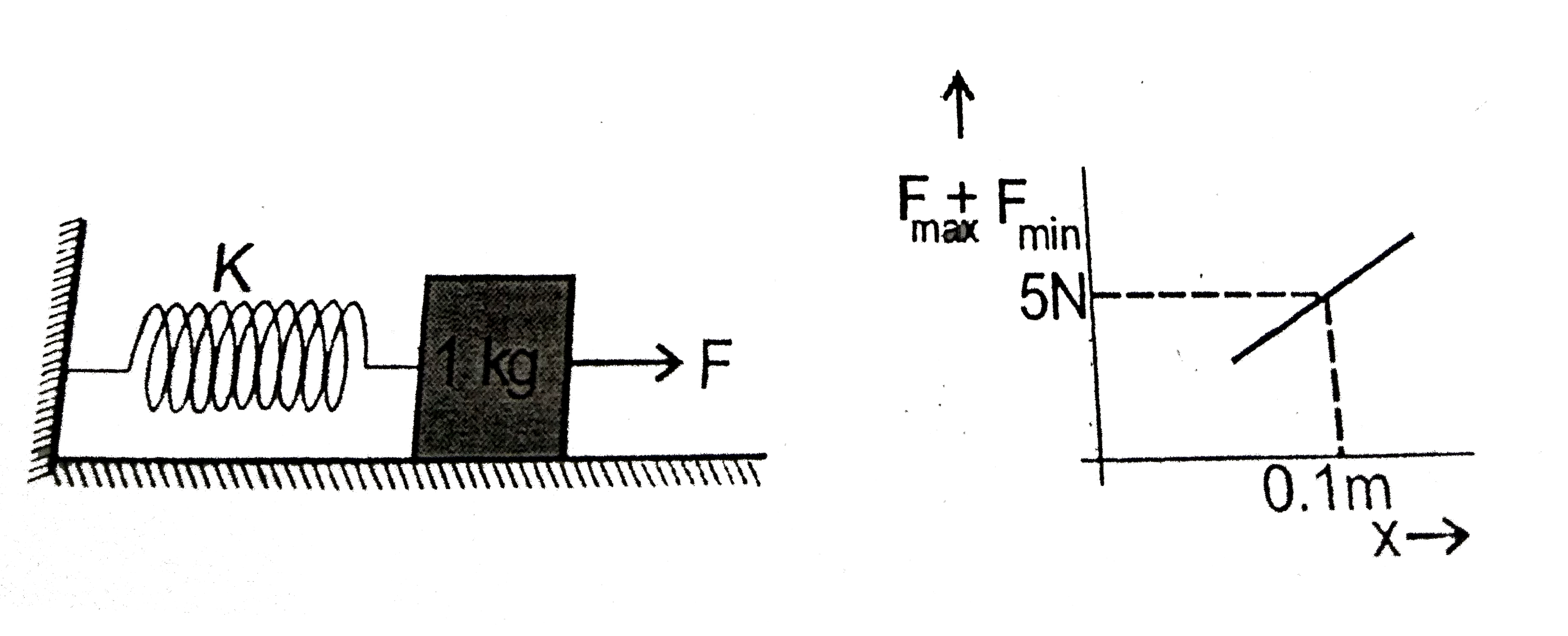
The value of Fmin, if x=3cm is :
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
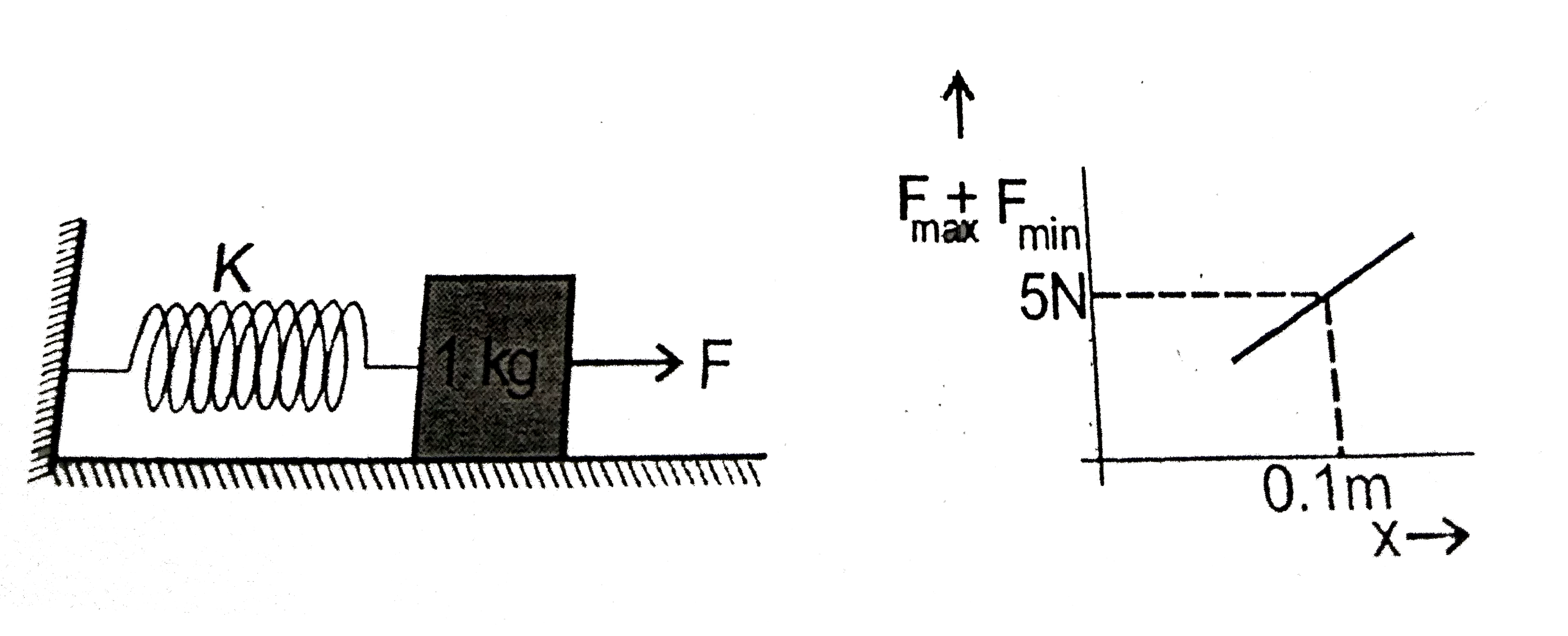
The value of Fmin, if x=3cm is :
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
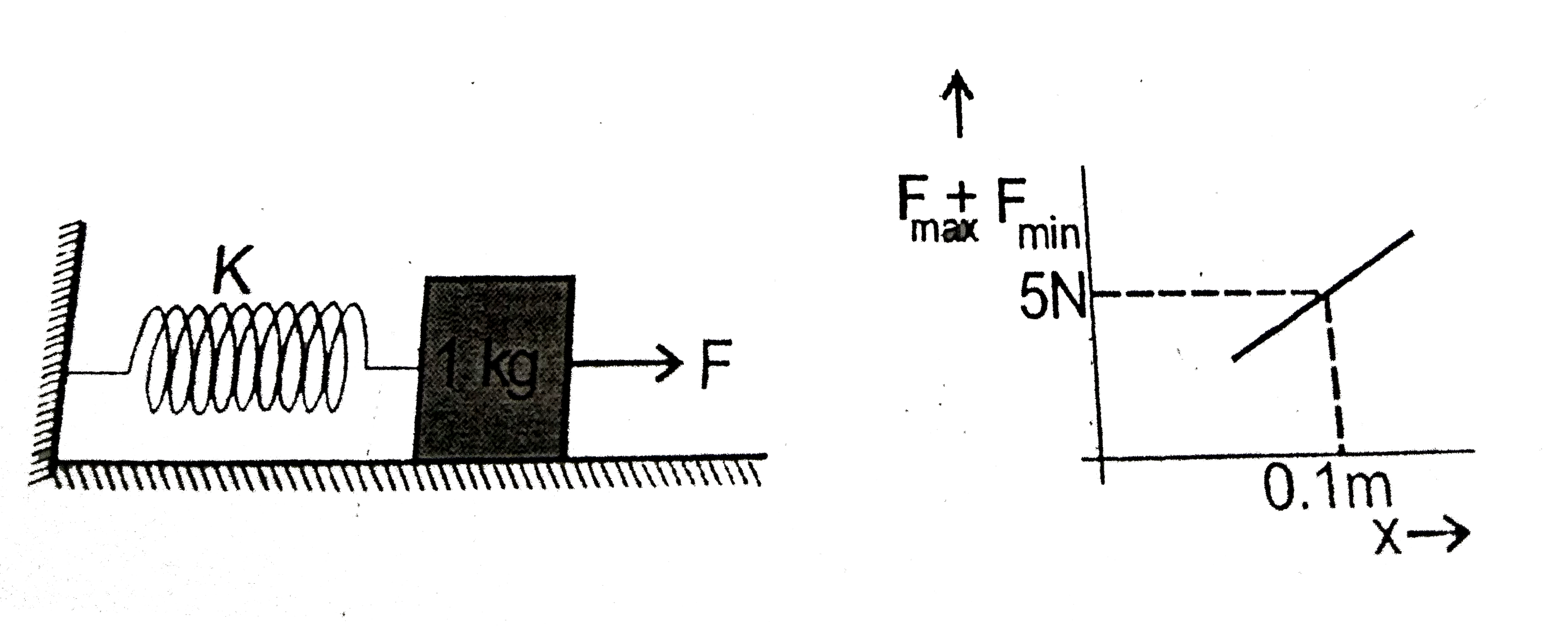
The coefficient of friction between the block and the horizontal surface is :
View Solution
