The tension in the strings T1 and T2 is:
55,55
53, 57
57, 53
None
The correct Answer is:b
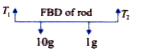
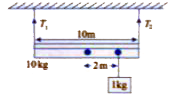
As the rod is in equilibrium
T1+T2=(10+1)g
⇒T1+T2=110…….(i)
Now, balancing torque about COM
T1×5+10×2=T2×5
⇒5(T2−T1)=20⇒T2−T1=4……..(i)
T1+T2=110 ............(ii)
From equations (i) and (ii)
2T2=114
T2=57N
T1=53N
Topper's Solved these Questions
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - MANDATORY EXERCISE
8 Videos
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - CONSOLIDATED EXERCISE
3 Videos
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - MANDATORY EXERCISE SET II
9 Videos
- SOUNDBOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
8 Videos
Similar Questions
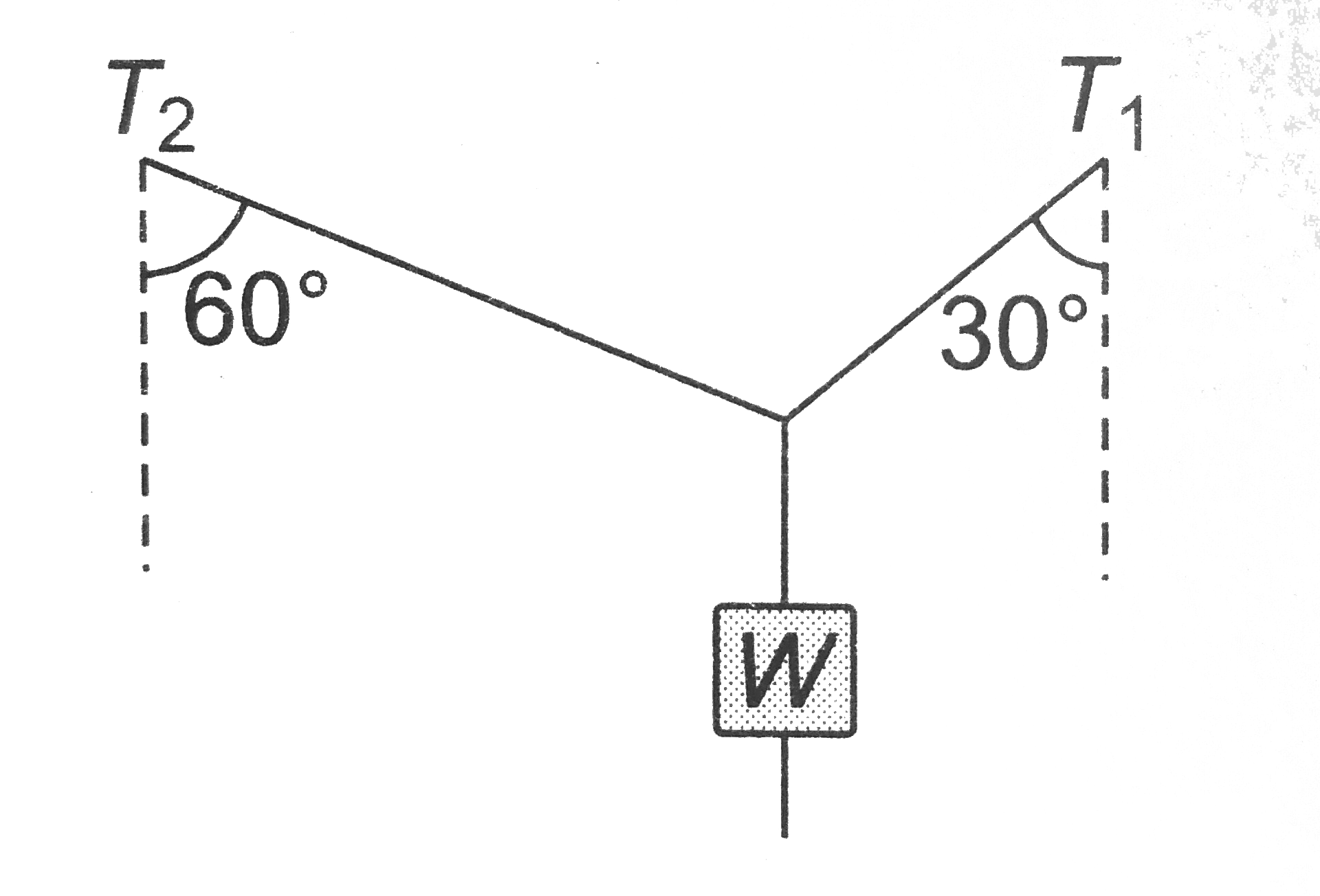
A weight W is supported by two strings inclined at 60∘ and 30∘ to the vertical. The tensions in the strings are T1 and T2 as shown. If these tensions in the strings are to be determined in terms of W using a triangle of force, which of these triangles should you draw? (block is in equilibrium)
View SolutionA pendulum is hanging from the ceiling of a cage. When the cage is moving up with certain acceleration and when it is moving down with the same acceleration, the tensions in the string are T1 and T2 respectively. When the cage moves horizontally with the same acceleration, the tension in the string is,
View Solution
Knowledge Check
A particle P of mass m is attached to a vertical axis by two strings AP and BP of legth l each. The separation AB=l, rotates around the axis with an angular velocity ω. The tension in the two string are T1 and T2. Then
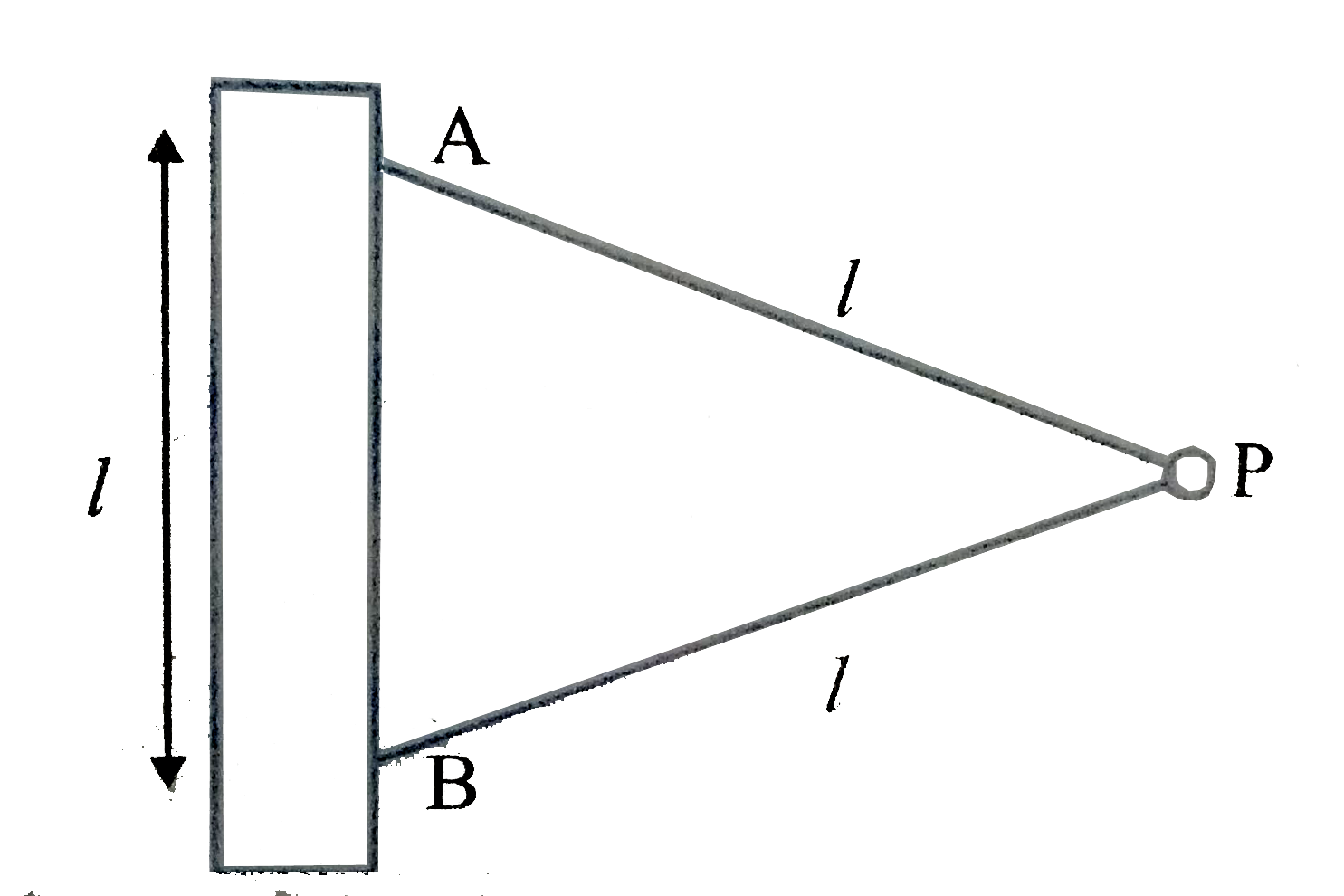 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remains taut only if ω≥√2g/l
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remains taut only if ω≥√2g/lA particle A of mass m is attached to a vertical axis by two stings PA and QA of lengths 3L and 4L , respectively. PQ=5L. A rotates around the axis with an angular speed ω. The tension in the two strings are T1 and T2.
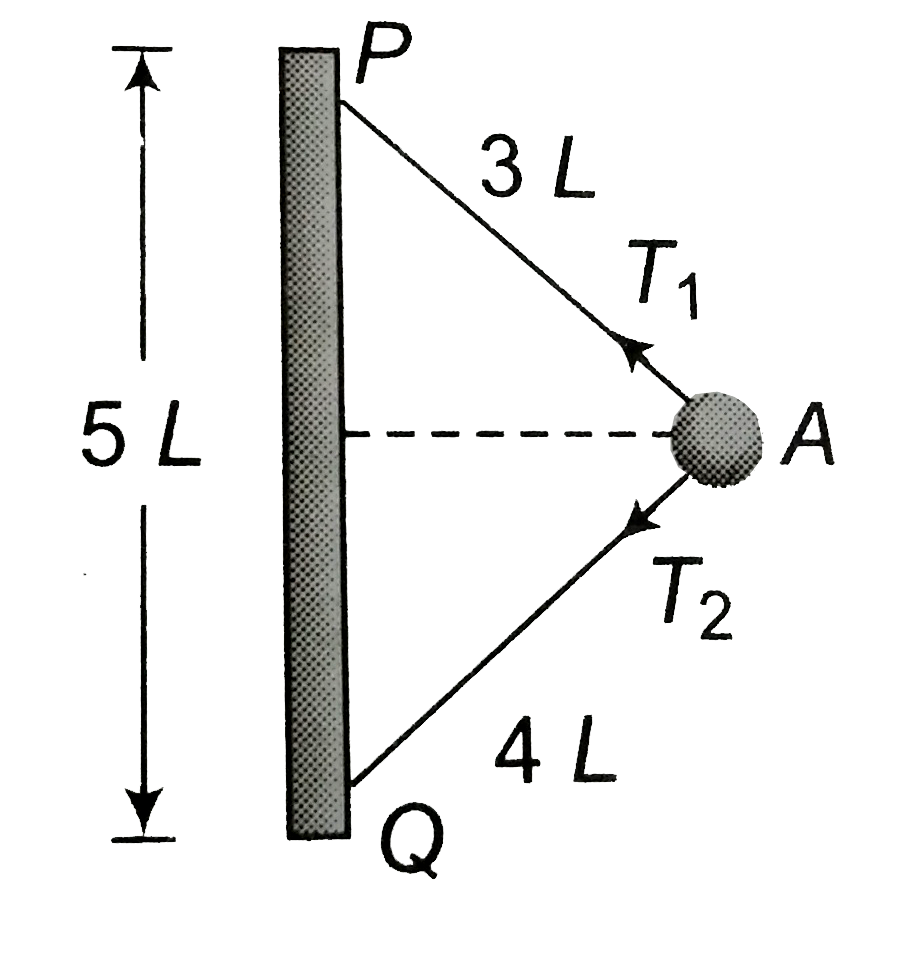
(i) T1=T2
(ii) 3T1−4T2=5mg
(iii) 4T1+3T2=12mω2LA(i)onlyB(i),(ii)C(i),(iii)D(ii),(iii)A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
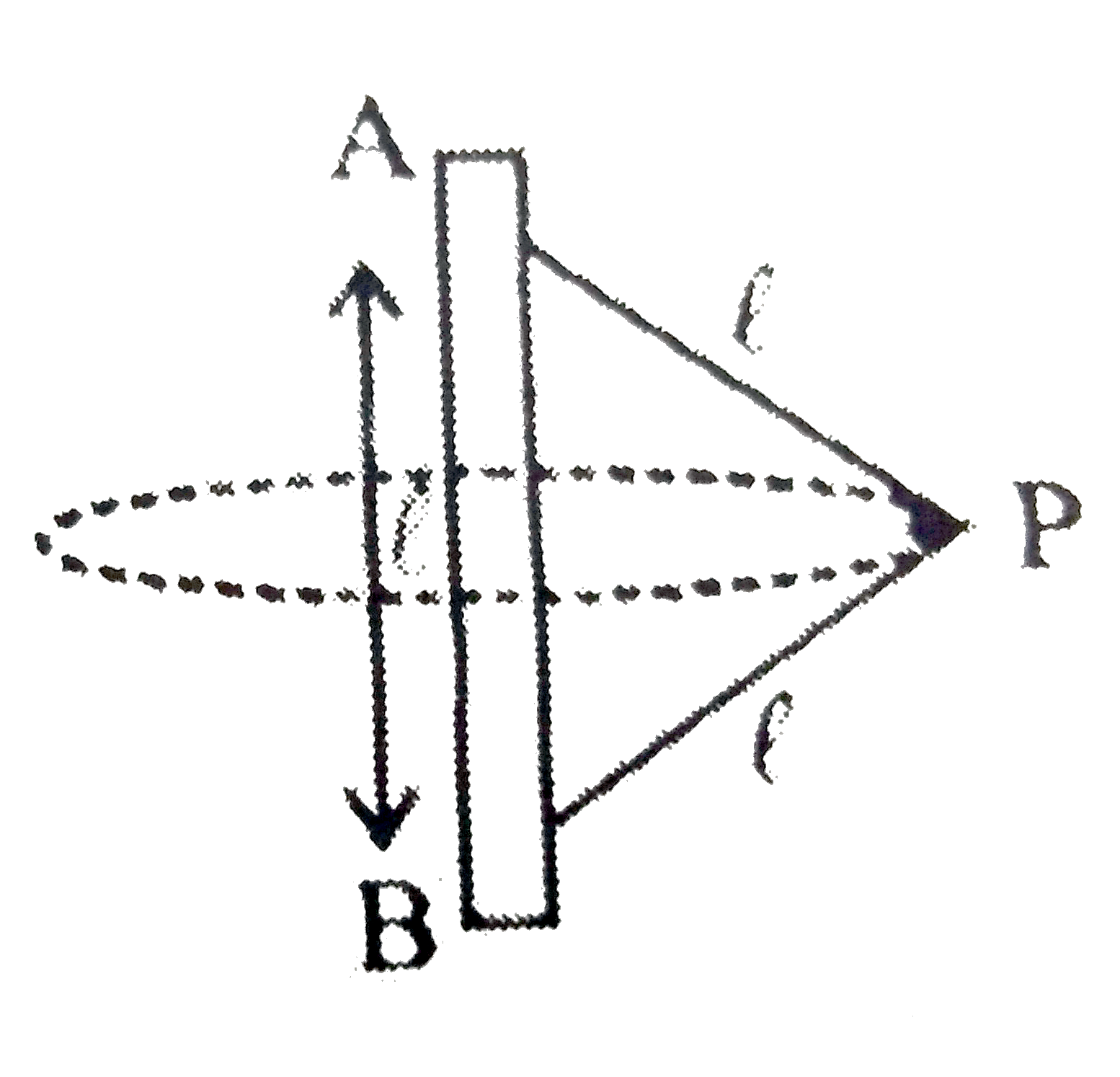 AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2gl
AT1=T2BT1+T2=mω2lCT1−T2=2mgDBP will remain taut only if ω≥√2gl
A particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2

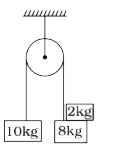
View SolutionA system is at rest as shown in figure. The tension in the string in T1. When the 2 kg block is removed, the system moves with some acceleration a and tension in string becomes T2 Find T1/T2 .
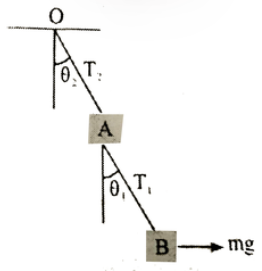
View SolutionIn the figure the masses of the blocks A and B are same and each equal to m. The tensions in the strings OA and AB are T2 and T1 respectively. The system is in equilibrium with a constant horizontal force mg on B. The tension T1 is :-
View SolutionA system is at rest as shown in figure. The tension in the string in T1. When the 2 kg block is removed, the system moves with some acceleration a and tension in string becomes T2 Find T1/T2 .

View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View Solution
