A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1 m behind the front axle. The force exerted by the level ground on each front wheel and each back wheel is (Take g:10ms−1)
4000 N on each front wheel, 5000 N on each back wheel
5000 N on each front wheel, 4000 N an each back wheel
4500N on each front wheel, 4500 N on each back wheel
3000 N on each front wheel, 6000 N on each back wheel
The correct Answer is:A
Here, mass of the car, M= 1800 kg
Distance between front and back axles = 1.8 m Distance of gravity G behind the front axle = 1 m
Let RF and RB be the forces exerted by the level ground on each front wheel and each back wheel.

For translational equilibrium,
2RF+2RB=Mg
or RF+RB=Mg2=1800×102=9000N.....(i)
(As there are two front wheels and two back wheels) For rotational equilibrium about G
(2RF)(1)=(2RB)(0.8)
RFRB=0.8=810=45⇒RF=45RB........(ii)
Substituting this in Eq. (i), we get
45RB+RB=9000 or 95RB=9000
RB=900×59=5000N
∴RF=45RB=45×5000N=4000N
Topper's Solved these Questions
- STATICSBOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - CHALLENGING EXERCISE
5 Videos
- SOUNDBOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
- UNITS AND MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
8 Videos
Similar Questions
A car weighs 1800 kg. The distance between its front and back axles is 1·8 m. Its centre of gravity is 1·05 m behind the front axle. Determine the force exerted by the level ground on each front and back wheel
View SolutionA car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
View Solution
Knowledge Check
A car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
A4000 N on each front wheel, 5000 N on each back wheelB5000 N on each front wheel, 4000 N an each back wheelC4500 N on each wheel, 4500 N on each back wheelD3000 N on each front wheel, 6000 N on each back wheelThe tricycle weighing 20 kg has a small wheel symmmetrically placed 1m behind the two large wheels, which are also 1m apart. If the center of gravity of machine is at a horizontal distance of 25 cm behind the front wheels and the rider whose weight is 40 kg is 10 cm behind the front wheels. Then, the thrust on each front wheel is
A255 NB90 NC200 ND400 N
A car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
View SolutionA car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force (in newton) exerted by the level ground on each front wheel.
View SolutionA uniform rod of length 1m having mass 1kg rests against a smooth wall at an angle of 30∘ with the ground. Calculate the force exerted by the ground on the rod. Take g=10ms−2.
View SolutionThe distance between the inner and outer wheels of a car is 1.75 m and its centre of gravity is 0-50 m above the ground. What is the maximum speed with which the car can negotiate a curve of radius of 40 m without overturning ?
View SolutionA cyclist rides round a curved path of radius 10m at a speed 18 kmph. If the cycle and the rider together have a mass of 100 kg, the firctional force the ground exerts on the wheel is (g = 10 ms2)
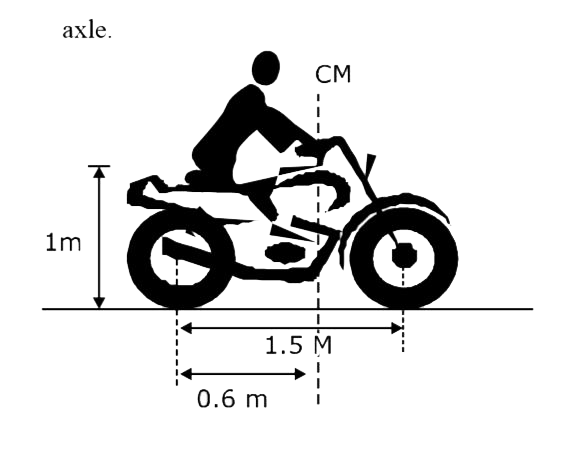
View SolutionThere is a man of mass 100 kg sitting on a motorbike of mass 150 kg. The distance of the axles of the wheels (wheelbase) is 1 . 5 m, the common mass center of the man and the motorbike is at a 1 m height above the ground level, and at a 0.6 m distance from the vertical line going through the rear axle.
What acceleration is needed to lift the front wheel?
View Solution
