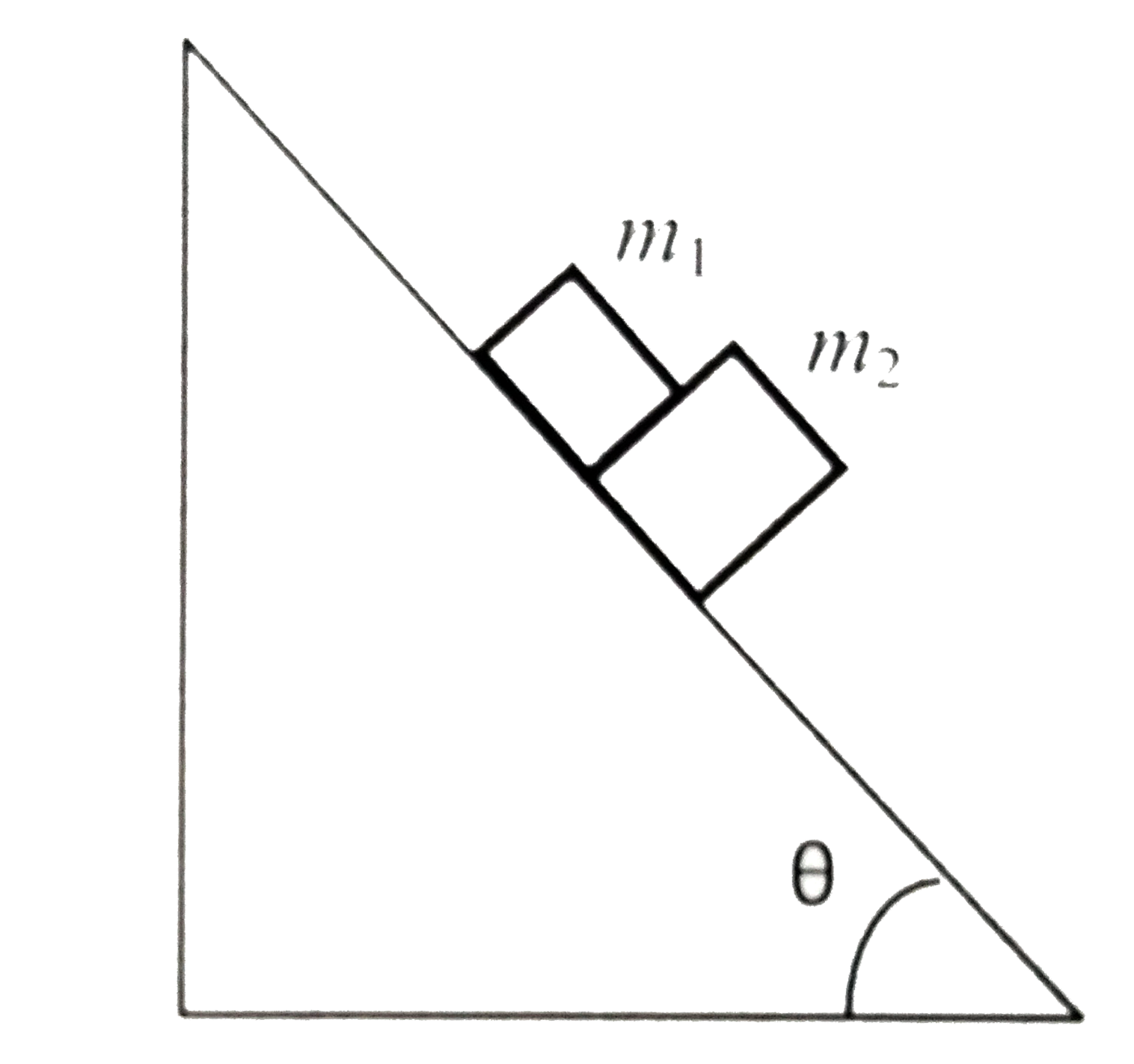
A block of mass m, = 1 kg and another mass m2=2 kg are placed together (see figure) on an inclined plane with angle of inclination θ. Various values of 0are given in List I. The coefficient of friction between the block m1 and the plane is always zero. The coefficient of static and dynamic friction between the block /w, and the plane are equal to μ=0.3 . In List II expressions for the friction on the block are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g.
![A block of mass m, = 1 kg and another mass m2 = 2 kg are placed together (see figure) on an inclined plane with angle of inclination theta. Various values of 0are given in List I. The coefficient of friction between the block m(1) and the plane is always zero. The coefficient of static and dynamic friction between the block /w, and the plane are equal to mu=0.3 . In List II expressions for the friction on the block are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g. [Useful information:tan(5.5^(@)) =0.1 tan (11.5^(@)) =0.2, tan (16.5^(@)) =0.3]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_JEE_PHY_IX_C10_E04_010_Q01.png)
[Useful information:tan(5.5∘)=0.1tan(11.5∘)=0.2,tan(16.5∘)=0.3]
p-1, q-1, r-1, s-3
p-2, q-2, r-2, s-3
p-2, q-2, r-2, s-4
p-2, q-2, r-3, s-3
The correct Answer is:D
Condition for not sliding,
fmax>(m1+m2)gsinθ
μN>(m1+m2)gsinθ
0.3m2gcosθ≥(1+2)10sinθ
0.3×2×10cosθ≥(1+2)10sinθ
6≥30tanθ
1/5≥tanθ⇒0.2≥tanθ
Now it is clear in case (P), (Q) it will not slip, friction is (m1+m2)gsinθ
⇒f=(m1+m2)gsinθ
In the case (R), (S) of they must slip so friction should be kinetic
i.e. μm2gcosθ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - STATICSEXERCISE - CHALLENGING EXERCISE5videos
STATICS
- BOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE10videos
SOUND
- BOOK - CENGAGE PHYSICSCHAPTER - UNITS AND MEASUREMENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES8videos
UNITS AND MEASUREMENT
Similar Questions
A block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together (see figure) on an inclined plane with angle of inclination θ. Various values of θ are given in List I. The coefficient of friction between the block m1 and the plane is always zero. The coefficient of static and dynamic friction between the block m2 and the plane are equal to μ=0.3 . In List II expressions for the friction on block m2 are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g
[Useful information :tan(5.5∘)≈0.1,tan(11.5∘)≈0.2,tan(16.5∘)≈0.3].
View SolutionA block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together (see figure) on an inclined plane with angle of inclination θ. Various values of θ are given in List I. The coefficient of friction between the block m1 and the plane is always zero. The coefficient of static and dynamic friction between the block m2 and the plane are equal to μ=0.3 . In List II expressions for the friction on block m2 are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g
[Useful information :tan(5.5∘)≈0.1,tan(11.5∘)≈0.2,tan(16.5∘)≈0.3].
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m1 = 1 kg and another mass m2=2 kg are placed together ( see figure) on an inclined plane with angle of inclination θ . Various values of θ are given in List I . The coefficient of friction between the block m1 and the plane is always zero. The coefficient of static and dynamic friction between the block m2 and the plane are equal to μ=0.3 . In List II expressions for the friction on the block m2 are given . Match the correct expression of the friction in List II with the angles given in List I , and choose the option . The acceleration due to gravity is denoted by g .
[Useful information : tan (5.5∘) = 0.1 , tan (11.5∘) = 0.2 , tan (16.5∘)=0.3]
ListIListIIP.θ=5∘1.m2gsinθQ.θ=10∘2.(m1+m2)gsinθR.θ=15∘3.μm2gcosθS.θ=20∘4.μ(m1+m2)gcosθ
AP-1 , Q-1 , R-1 , S-3BP-2 , Q-2 ,R-2 , S-3CP-2 , Q-2 , R-2 , S- 4DP-2 , Q-2 , R-3 , S-3 - Question 2 - Select One
A block of mass m1=1kg and another mass m2=2kg are placed together(see figure) on an inclined plane with angle of inclination θ varius value of θ are given in list 1 The coefficient of friction between the block m1 and the plank is always zero The coefficient of static and dynamic friction between the block m2 and the plank are equal to μ=0.3 In List II experssions for the friction the block m2 are given Match the correct experssions of the frictionless in List II with the angle given in list 1 and choice the correct option The acceleration due too gravity detented by g
[Useful information tan(5.5∘)=0.1tan(11.5∘)=0.2tan(16.5∘)=0.3]
List I P. θ=5∘ Q. θ=10∘
R. θ=15∘ S. θ=20∘
List 2
1.m2gsinθ 2.(m1+m2)gsinθ
3.μm2gcosθ 4. μ(m1+m2)gcosθAP−1,Q−1,R−1,S−3BP−2,Q−2,R−2,S−3CP−2,Q−2,R−2,S−4DP−2,Q−2,R−3,S−3 - Question 3 - Select One
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A block of mass m1=1kg and another mass m2=2kg are placed together(see figure) on an inclined plane with angle of inclination θ varius value of θ are given in list 1 The coefficient of friction between the block m1 and the plank is always zero The coefficient of static and dynamic friction between the block m2 and the plank are equal to μ=0.3 In List II experssions for the friction the block m2 are given Match the correct experssions of the frictionless in List II with the angle given in list 1 and choice the correct option The acceleration due too gravity detented by g
[Useful information tan(5.5∘)=0.1tan(11.5∘)=0.2tan(16.5∘)=0.3]
List I P. θ=5∘ Q. θ=10∘
R. θ=15∘ S. θ=20∘
List 2
1.m2gsinθ 2.(m1+m2)gsinθ
3.μm2gcosθ 4. μ(m1+m2)gcosθView SolutionThe coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution