A horizontal rod suspended from two wires of same length and cross - section. Their Young's modulus are Y1 and Y2 respectively. The equivalent Young's modulus will be

Y1+Y22
Y1+Y2
2(Y1+Y2)
(Y1+Y2)
The correct Answer is:A
Say the equivalent Young.s modulus is Y and area of cross section be 2A.
As we know extended wires behave like springs
[F=AY(ΔL)L is equivalent to F=kx]
For parallel combination K1+K2=Keq
⇒AY1L+AY2L=(2A)YL
⇒Y=Y1+Y22
Topper's Solved these Questions
- ELASTICITYBook:CENGAGE PHYSICSChapter:ELASTICITYExercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
- ELASTICITYBook:CENGAGE PHYSICSChapter:ELASTICITYExercise:CONSOLIDATED EXERCISE
Explore 5 Videos
- DESCRIPTION OF MOTIONBook:CENGAGE PHYSICSChapter:DESCRIPTION OF MOTIONExercise:OLYMPIAD AND NTSE LEVEL EXERCISE
Explore 10 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
Explore 1 Video
Similar Questions
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
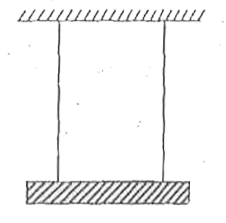
View SolutionTwo wires of equal length and cross sectional area suspended as shown in
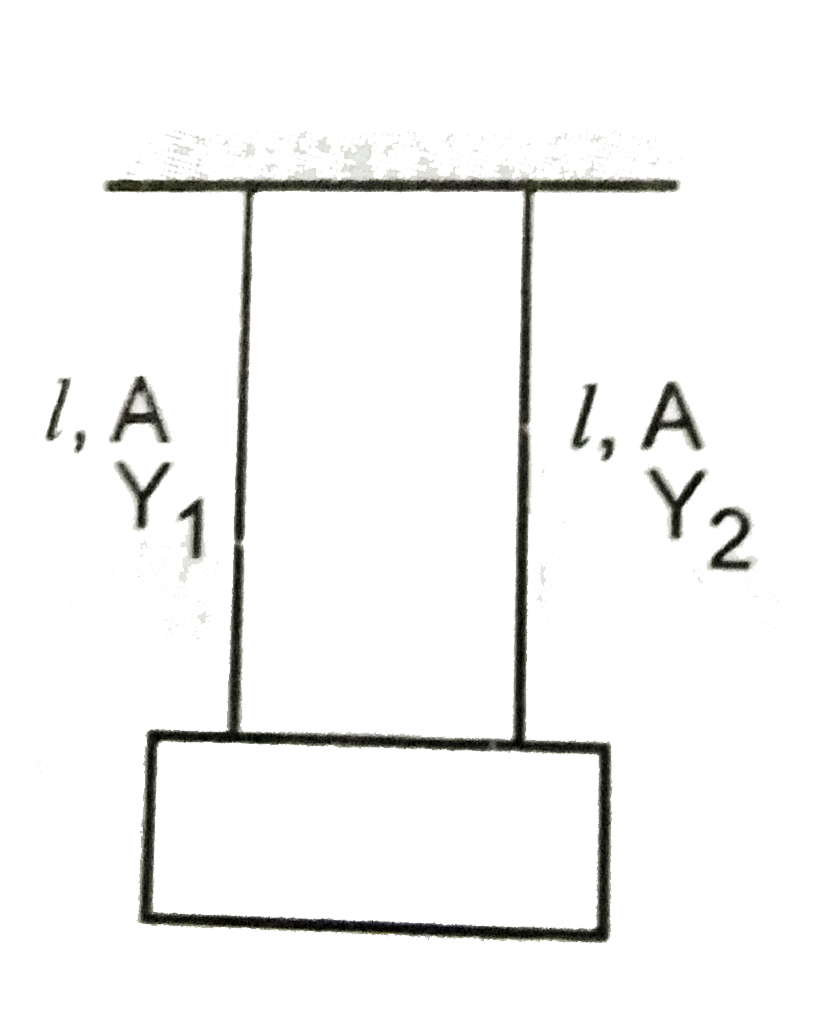
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution
Knowledge Check
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be
 AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2If the length of a wire is doubled, then its Young's modulus
Abecome doubleBbecome halfCincreases but becomes not exactly doubleDremains unchanged
A force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionTwo wires of equal dimensions and young's modulus Y1 and Y2 are connected end to end. What is the equivalent young's modulus for the combination?
View SolutionThe Young's modulus of a wire of length L and radius r is Y. If the length and radius is reduced to L/2 and r/2 respectively, then its Young' modulus will be
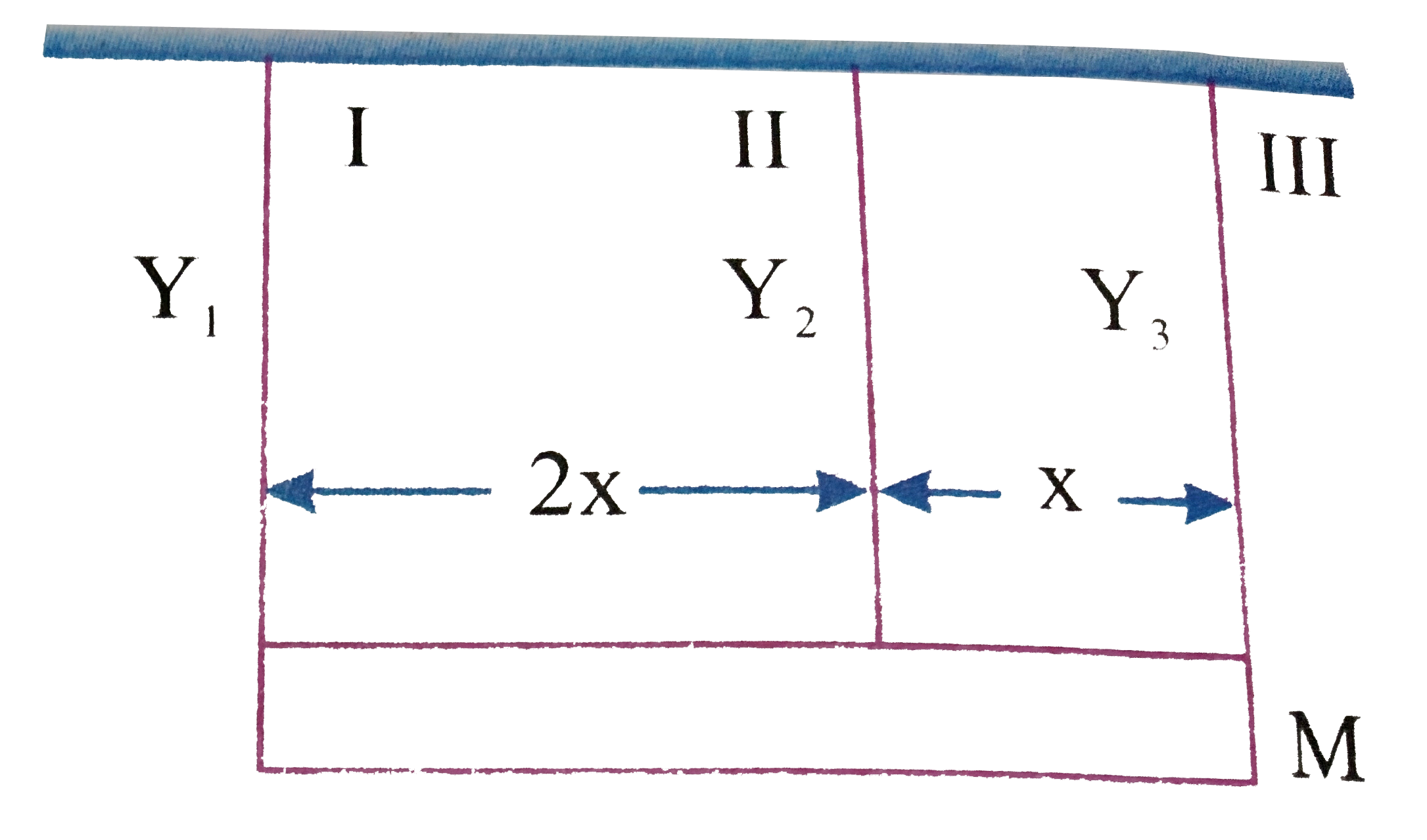
View SolutionThree vertical wires, I,II and III are supporting a block of mass M in horizontal positon. The wires are to equal length and cross-sectional area. It is given that Young's modulus of wire II,Y2=Y3 (Yong's modulus of wire III). The wire I and III and attached at extreme ends of the block.
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View Solution
