Use the graph to find the limits (if it exists). If the limit does not exist, explain why?
limx→2f(x) where f(x)={4−x,x≠20,x=2
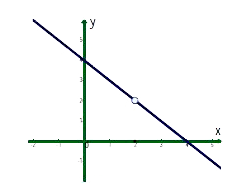
The correct Answer is:2
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.2
14 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.3
12 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - Illustration
3 Videos
- CONIC SECTIONSBOOK - NCERT TAMILCHAPTER - CONIC SECTIONSEXERCISE - Miscellaneous Exercise
8 Videos
- DIFFERENTIAL CALCULUS-DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION BOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS-DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION EXERCISE - EXERCISE 10.5
25 Videos
Similar Questions
Find k so that (lim)x→2 f(x) may exist, where f(x)={2x+3, x≤2x+k,x>2
View SolutionEvaluate the following limits, if they exist :
limx→2(3−x)
View SolutionEvaluate the following limits, if they exist :
limx→24
View SolutionWhich of the following limit exists finitely ? limx→0+(x)logex
View Solutionf(x)=x,x<0,1,x=0,x2,x>0 then find limx→0f(x) if exists
View SolutionEvaluate the limits, if existlimx→0(xex−11−cosx)
View SolutionEvaluate the following limits, if they exist :
limx→3[x(x+1)]
View SolutionIf f(x) = [x] – [x/4] , x ∈ R, where [x] denotes the greatest integer function, then :
(1) lim f(x) (x→4-)exists but lim f(x) (x→4+) does not exist.
(2) Both lim f(x) (x→4-) and lim f(x) (x→4+) exist but are not equal.
(3) lim f(x) (x→4+) exists but lim f(x) (x→4-) does not exist.
(4) f is continuous at x = 4.
View SolutionEvaluate the limits, if existlimx−>0loge(1+2x)x
View SolutionEvaluate the limits, if exist limx→0e2+x−e2x.
View Solution
