Use the graph to find the limits (if it exists). If the limit does not exist, explain why?
limx→31x−3
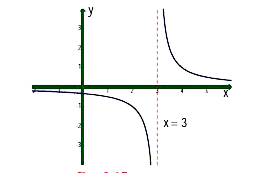
Text Solution
The correct Answer is:does not exis
|
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.2
14 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.3
12 Videos
- DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYBOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - Illustration
3 Videos
- CONIC SECTIONSBOOK - NCERT TAMILCHAPTER - CONIC SECTIONSEXERCISE - Miscellaneous Exercise
8 Videos
- DIFFERENTIAL CALCULUS-DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION BOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS-DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION EXERCISE - EXERCISE 10.5
25 Videos
Similar Questions
Evaluate the limits, if exist limx→0esinx−1x.
View SolutionEvaluate the limits, if existlimx→3ex−e3x−3
View SolutionEvaluate the limits, if existlimx→0(xex−11−cosx)
View SolutionEvaluate the limits, if exist limx→0loge(1+2x)x.
View SolutionEvaluate the limits, if exist limx→0e4x−1x.
View Solutionwhich of the following limit do not exist limx→1x3+x−2x3−x2−x+1
View SolutionEvaluate the limits, if exist(lim)x→0log(1+x3)sin3x
View SolutionWhich of the following limit exists finitely ? limx→0+(x)logex
View SolutionEvaluate the following limits :
limx→139x2−13x−1
View SolutionEvaluate the limits, if exist limx→0log(1+x3)sin3x
View Solution
