Consider the given question and decide which of the following statements is sufficient to answer the question. If X scored an average of 50 marks in History, Language and Science, how much did he score in Science? Statements: 1. His average score in History and Language is 25. 2. He got 30 marks in Language.
Both 1 and 2 are sufficient to answer the given question.
2 alone is sufficient while 1 alone is not sufficient to answer the given question.
1 alone is sufficient while 2 alone is not sufficient to answer the given question.
Neither 1 nor 2 is sufficient to answer the given question.
Step by step video & image solution for Consider the given question and decide which of the following statements is sufficient to answer the question. If X scored an average of 50 marks in History, Language and Science, how much did he score in Science? Statements: 1. His average score in History and Language is 25. 2. He got 30 marks in Language. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
The average marks of English and History subjects is 55. His average marks in English and Science is 65. What is the difference between his marks in History and Science?
03:13View SolutionA student scored 32% marks in science subjects out of 300. How much should he score in language papers out of 200 if he is to get overall 46% marks?
02:11View SolutionThe bar graph shows average marks scored in a 100 mark Science exam by students of 7 divisions of Standard X. Study the diagram and answer the following questions.
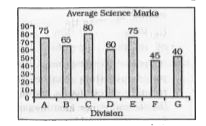
Marks of division F were lesser than that of Division C by03:04View SolutionThe bar graph shows average marks scored in a 100 mark Science exam by students of 7 divisions of Standard X. Study the diagram and answer the following questions.
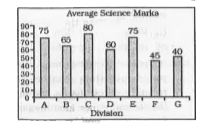
What is the raio of average marks scored by Division D to Division A?02:51View SolutionArnav scored 63 marks in English, 57 in Hindi, 82 in Mathematics, 55 in Social Science and x in Science. If the average he scored is 60, find the average of best four of them.
02:22View SolutionThe bar graph shows average marks scored in a 100 marks History exam by students of 7 divisions of Standard x. Study the diagram and answer the following questions.
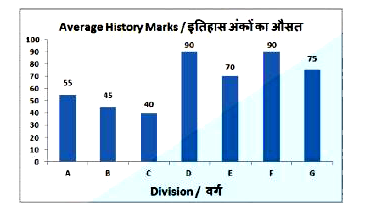
Which division scored the second lowest marks ?01:09View SolutionThe bar graph shows average marks scored in a 100 marks Science exam by student of 7 divisions of Standard X. Study the diagram and answer the following questions.
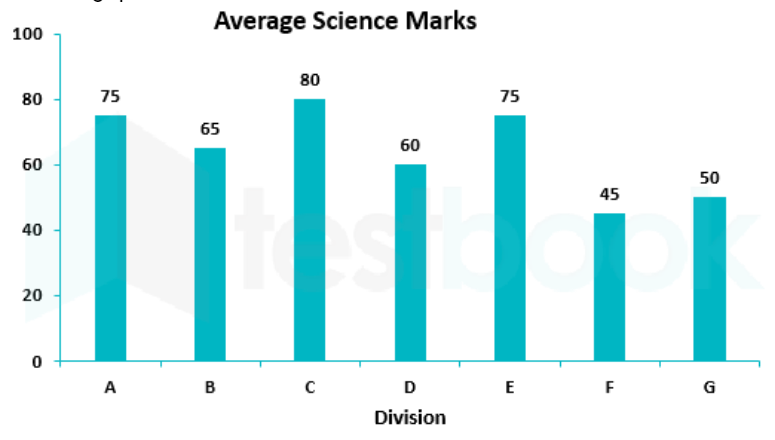
Which division scored the second lowest marks?01:18View SolutionStudy the data carefully and answer the following questions. Find the average of the marks scored by Aditya in English, Hindi and Science together?
02:02View Solution
