A particle moving with constant acceleration of $2 m / s^{2}$ due west has an initial velocity of 9 m/s due east. Find the distance covered in the fifth second of its motion.

Text Solution

Verified by Experts

Initial velocity u = +9 m/s Acceleration $a = - 2 m / s^{2}$

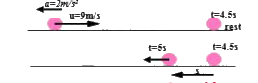
In this problem, acceleration’s direction is opposite to the velocity’s direction. Let .t. be the time taken by the particle to reach a point where it makes a turn along the straight line. We have, v = u + at
O = 9 – 2 t
We get, t = 4.5s
Now let us find the distance covered in 1/2 second i.e. from 4.5 to 5second
Let u = 0 at t = 4.5 sec.
Then distance covered in 1/2 s
$s = \frac{1}{2} a t^{2}$
$s = \frac{1}{2} \times 2 \times {[\frac{1}{2}]}^{2}$
$= \frac{1}{4} m$
Total distance covered in fifth second of its motion is given by
$S_{0} = 2 s = 2 (1 / 4) = 1 / 2 m$ .

Updated on:21/07/2023

A particle is moving on a straight line with constant retardation of $1 m / s^{2}$ . Its initial velocity is $10 m / s$ .
AThe distance travelled by the particle till it comes to rest is 50 m.
BThe average velocity till it comes to rest is $5 m / s$ .
CIt comes to rest in 5 sec.
DIts velocity after 5 sec is $5 m / s$
A particle has an initial velocity of $5.5 m s^{- 1}$ due east and a constant acceleration of $1 m s^{- 2}$ due west. The distance covered by the particle in sixth second of its motion is.
A0
B0.25 m
C0.5 m
D0.75 m
A particle has an initial velocity of $9 m / s$ due east and a constant acceleration of $2 m / s^{2}$ due west. The displacement coverd by the particle in the fifth second of its motion is :
Azero
B0.5m
C2m
DNone