What is the speed of the body moving with uniform acceleration at the midpoint of two points on a straight line, where the speeds are u and v respectively?
Let .a. be the constant acceleration and s be the distance between the two points, From equation of motion
v2−u2=2as ……..(1)

Let v0 be the speed of the body at midpoint ‘M’ of the given points. Applying the same equation used above, we get
v20−u2=2as2
from (1), we get
v20−u2=v2−u22
v20=v2−u22+u2
v20=v2−u2+2u22
v0=√v2+u22
Topper's Solved these Questions
- MOTIONBOOK - NCERT TELUGUCHAPTER - MOTIONEXERCISE - LET US IMPROVE OUR LEARNING (APPLICATION OF CONCEPTS)
3 Videos
- MOTIONBOOK - NCERT TELUGUCHAPTER - MOTIONEXERCISE - Improve your learning
8 Videos
- MOTIONBOOK - NCERT TELUGUCHAPTER - MOTIONEXERCISE - THINK AND DISCUSS
14 Videos
- LAWS OF MOTIONBOOK - NCERT TELUGUCHAPTER - LAWS OF MOTIONEXERCISE - IMPROVE YOUR LEARNING
6 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - NCERT TELUGUCHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - LET US IMPROVE OUR LEARNING (APPLICATION OF CONCEPTS)
1 Videos
Similar Questions
For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionThe speed of a body moving with uniform acceleration is u. This speed is doubled while covering a distance S. When it covers an additional distance S, its speed would become
View Solution
Knowledge Check
For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
A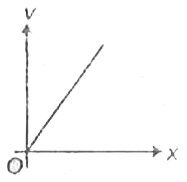 B
B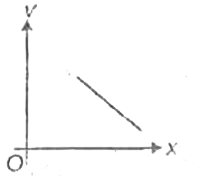 C
C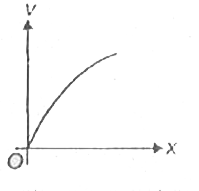 D
D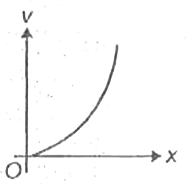
For body moving with uniform acceleration a, initial and final velocities in a time interval t are u and v respectively. Then its average velocity in the time interval t is
A(v+at)B(v−at2)C(v−at)D(u−at2)The speed of a body moving with uniform acceleration is u. This speed is doubled while covering a distance S. When it covers an additional distance S, its speed would become
A√3uB√5uC√11uD√7u
The speed of a body moving with uniform acceleration is u. This speed is doubled while covering a distance S. When it covers an additional distance S, its speed would become
View SolutionRelative speed of two bodies moving in opposite direction with speed u and v m/s.
View SolutionRelative speed of two bodies moving in same direction with speed u and v m/s: where (u>v)
View SolutionRelative speed of two persons moving with u m/s and v m/s in same direction where u>v
View SolutionAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View Solution
