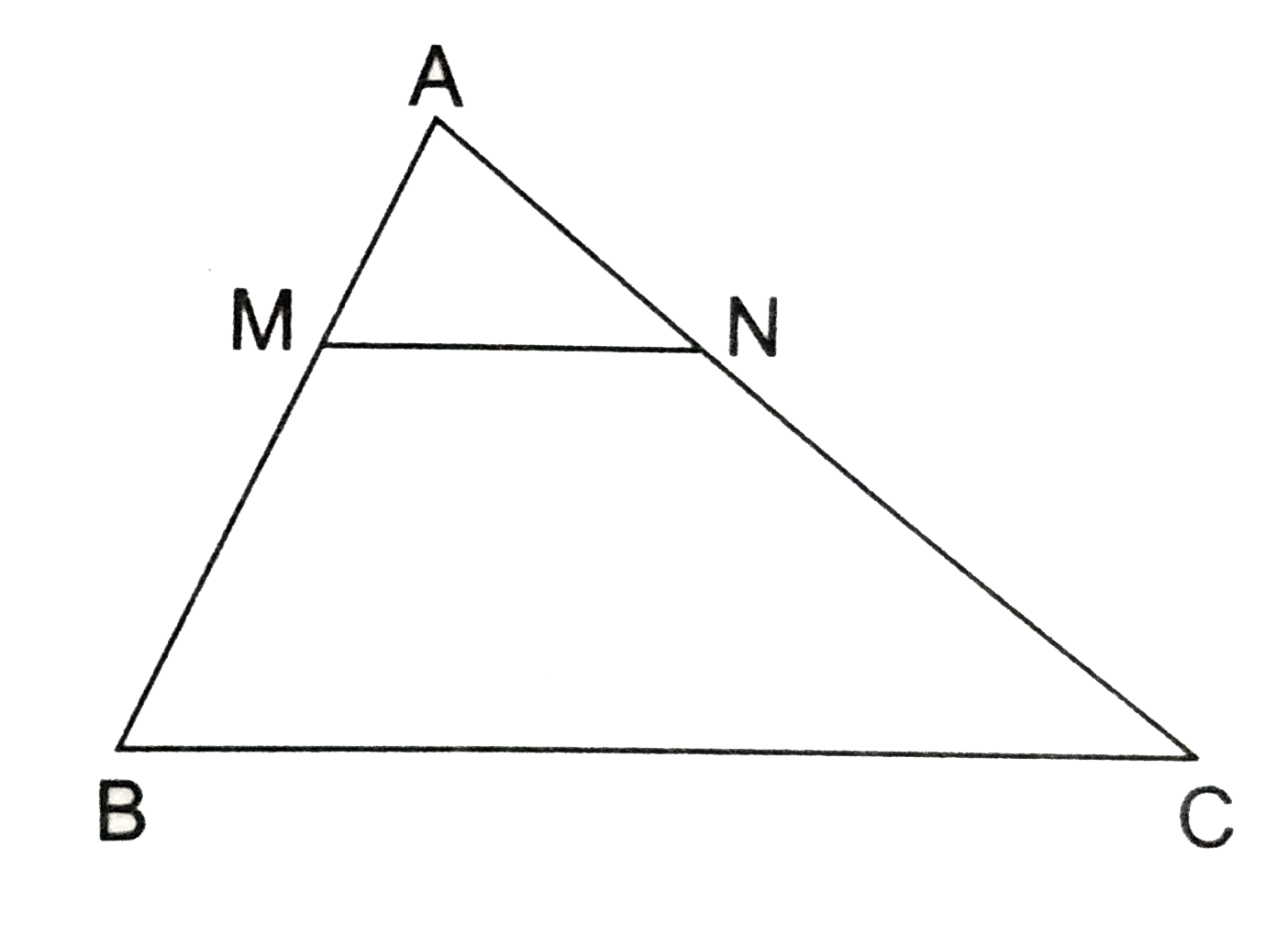
In the ΔABC , MN||BC and AM : : MB = 13.
Then, ar(ΔAMN)ar(ΔABC)=?
9:1
1:16
2:3
3:2
The correct Answer is:B
To solve the problem, we need to find the ratio of the areas of triangles AMN and ABC given that MN is parallel to BC and the ratio AM:MB = 1:3.
1. Understanding the Given Information:
- We have triangle ABC.
- MN is a line parallel to BC.
- The ratio of segments AM to MB is given as 1:3.
2. Using the Property of Similar Triangles:
- Since MN is parallel to BC, triangles AMN and ABC are similar by the Basic Proportionality Theorem (or Thales' theorem).
- This means that the corresponding angles of triangles AMN and ABC are equal.
3. Setting Up the Ratios:
- From the given ratio AM:MB = 1:3, we can express the lengths of AM and MB in terms of a variable. Let AM = x and MB = 3x.
- Therefore, the total length AB = AM + MB = x + 3x = 4x.
4. Finding the Ratio of Corresponding Sides:
- The ratio of the corresponding sides of triangles AMN and ABC is:
AMAB=x4x=14
5. Calculating the Ratio of Areas:
- The ratio of the areas of similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we have:
ar(ΔAMN)ar(ΔABC)=(AMAB)2=(14)2=116
6. Final Answer:
- Thus, the ratio of the area of triangle AMN to the area of triangle ABC is:
ar(ΔAMN)ar(ΔABC)=116
- We have triangle ABC.
- MN is a line parallel to BC.
- The ratio of segments AM to MB is given as 1:3.
- Since MN is parallel to BC, triangles AMN and ABC are similar by the Basic Proportionality Theorem (or Thales' theorem).
- This means that the corresponding angles of triangles AMN and ABC are equal.
- From the given ratio AM:MB = 1:3, we can express the lengths of AM and MB in terms of a variable. Let AM = x and MB = 3x.
- Therefore, the total length AB = AM + MB = x + 3x = 4x.
- The ratio of the corresponding sides of triangles AMN and ABC is:
AMAB=x4x=14
- The ratio of the areas of similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we have:
ar(ΔAMN)ar(ΔABC)=(AMAB)2=(14)2=116
- Thus, the ratio of the area of triangle AMN to the area of triangle ABC is:
ar(ΔAMN)ar(ΔABC)=116
Topper's Solved these Questions
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - SECTION-C
10 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART-A (SECTION-I)
21 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART - B (SECTION - V)
4 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - V)
8 Videos
- SAMPLE PAPER 9BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9EXERCISE - SECTION C
10 Videos
Similar Questions
Knowledge Check
In a ΔABC,AB=ACandAD⊥BC, then:
AAB<ADBAB>ADCAB=ADDAB≤ADIn ΔABC, D and E are points on AB and AC respectively such that DE is parallel to BC. If AD= 2 cm, BD = 3 cm, then ar(ΔADE)ar(ΔABC) is
A49B1681C425D25In ΔABC,AD is the bisector of ∠A . Then , ar(ΔABD)ar(ΔACD)=
AAB2AC2BABACCBMCMDNone of these
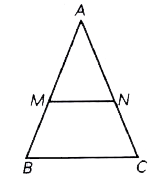
In the figure, MN∣∣BC and AM:MB=1:3, then ar(△AMN)ar(△ABC)=…………..
View SolutionIn ΔABC,AB+BC>
View SolutionIn Figure 1, PQ || BC and AP : PB = 1 : 2.find the ratio of arΔAPQarΔABC
View SolutionIt is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
View SolutionIt is given that ΔABC−ΔPQR, with BCQR=14. Then arΔPQRarΔABC is equal to:
View Solution