In (ΔABC) , MN∣∣BC and AM:AB=13. Then find the ratio of ar(ΔAMN)ar(ΔABC)
1:4
1:9
4:1
9:1
The correct Answer is:B
To solve the problem, we need to find the ratio of the areas of triangles AMN and ABC given that MN is parallel to BC and that AM:AB=13.
1. Identify the Similar Triangles:
Since MN is parallel to BC, triangles AMN and ABC are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This means that the angles of triangle AMN are equal to the corresponding angles of triangle ABC.
Hint: Remember that parallel lines create corresponding angles that are equal.
2. Set Up the Ratio of Sides:
From the problem, we know that AM:AB=13. This means that if we let AM=x, then AB=3x.
Hint: Use the given ratio to express the lengths in terms of a variable.
3. Use the Property of Similar Triangles:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(ΔAMN)ar(ΔABC)=(AMAB)2
Hint: Recall that the area ratio of similar triangles is the square of the ratio of their corresponding sides.
4. Substitute the Known Values:
We know from the problem that AMAB=13. Substituting this into our area ratio gives:
ar(ΔAMN)ar(ΔABC)=(13)2=19
Hint: Make sure to square the ratio when calculating the area ratio.
5. Conclusion:
Therefore, the ratio of the area of triangle AMN to the area of triangle ABC is:
ar(ΔAMN)ar(ΔABC)=19
Final Answer:
The ratio of ar(ΔAMN) to ar(ΔABC) is 19.
Since MN is parallel to BC, triangles AMN and ABC are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This means that the angles of triangle AMN are equal to the corresponding angles of triangle ABC.
From the problem, we know that AM:AB=13. This means that if we let AM=x, then AB=3x.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(ΔAMN)ar(ΔABC)=(AMAB)2
We know from the problem that AMAB=13. Substituting this into our area ratio gives:
ar(ΔAMN)ar(ΔABC)=(13)2=19
Therefore, the ratio of the area of triangle AMN to the area of triangle ABC is:
ar(ΔAMN)ar(ΔABC)=19
The ratio of ar(ΔAMN) to ar(ΔABC) is 19.
Topper's Solved these Questions
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-B
20 Videos
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C
10 Videos
- SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -C
10 Videos
- SAMPLE PAPER 10 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
Similar Questions
Knowledge Check
In figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
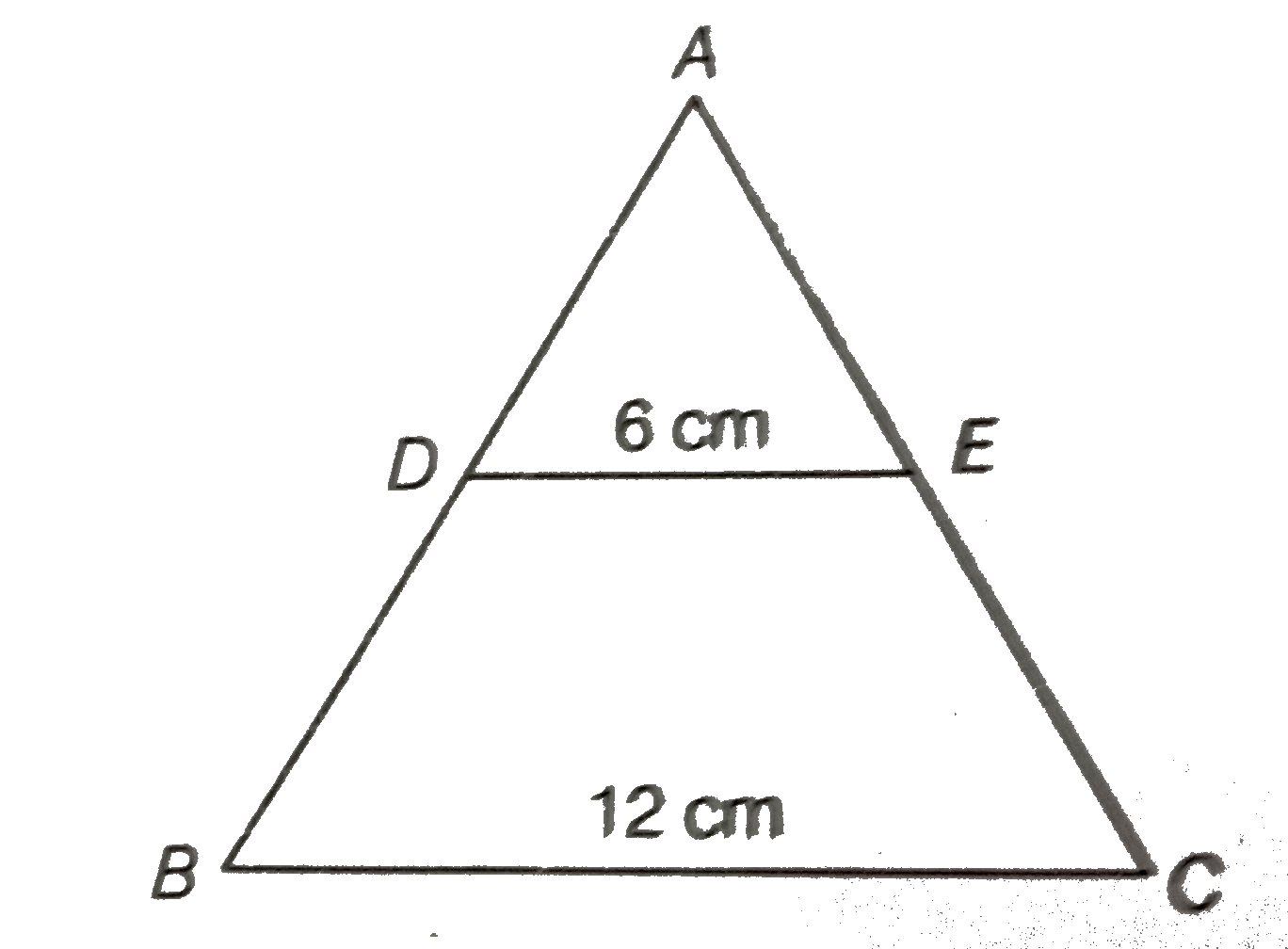 A1:3B1:2C2:5D3:5
A1:3B1:2C2:5D3:5In ΔABC,BC=ABand∠B=80∘. Then, ∠A=?
A50∘B40∘C100∘D80∘
In ΔABC,AB+BC>
View SolutionIn ΔABC,B - D - C and BD = 7, BC = 20, then find the ratio
A(ΔABD)A(ΔABC)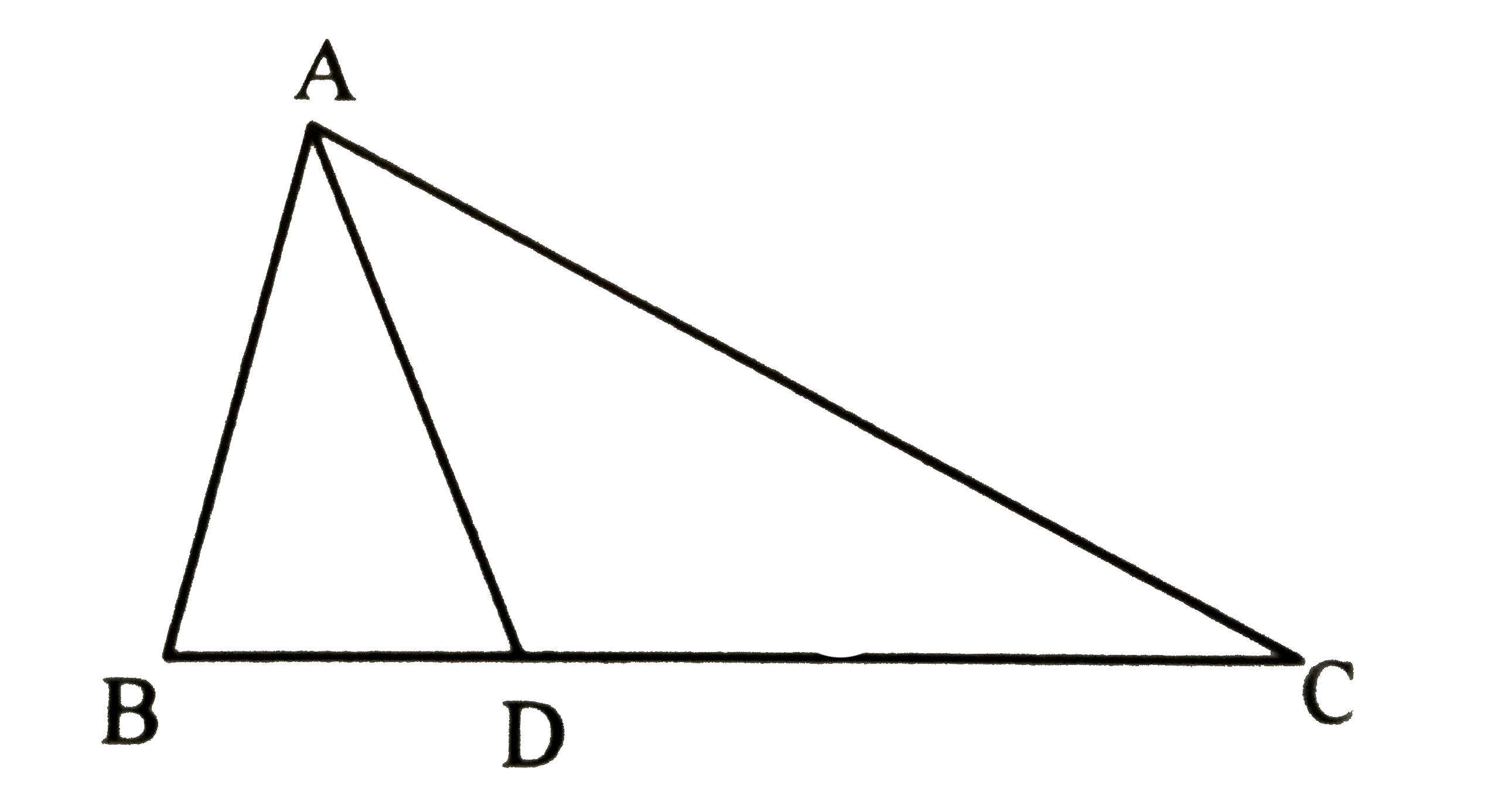
View SolutionIn ΔABC,B−D−C and BD=7,BC=20, then find followig ratios:

A(ΔABD)A(ΔADC)
A(ΔABD)A(ΔABC)
A(ΔADC)A(ΔABC)
View SolutionIn the figure, BC=7 and BD=3 then write the ratio of A(ΔADC):A(ΔABC).
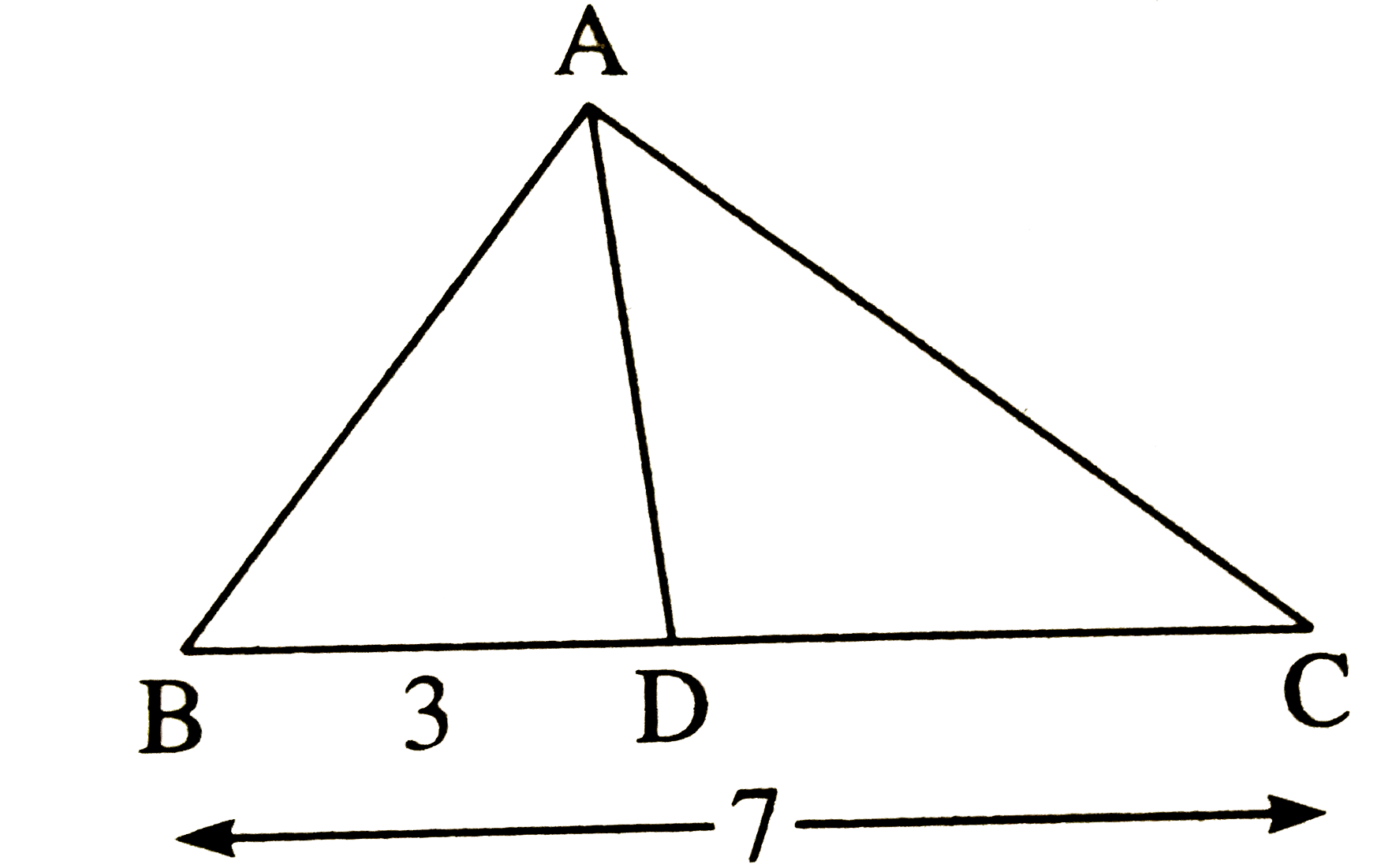
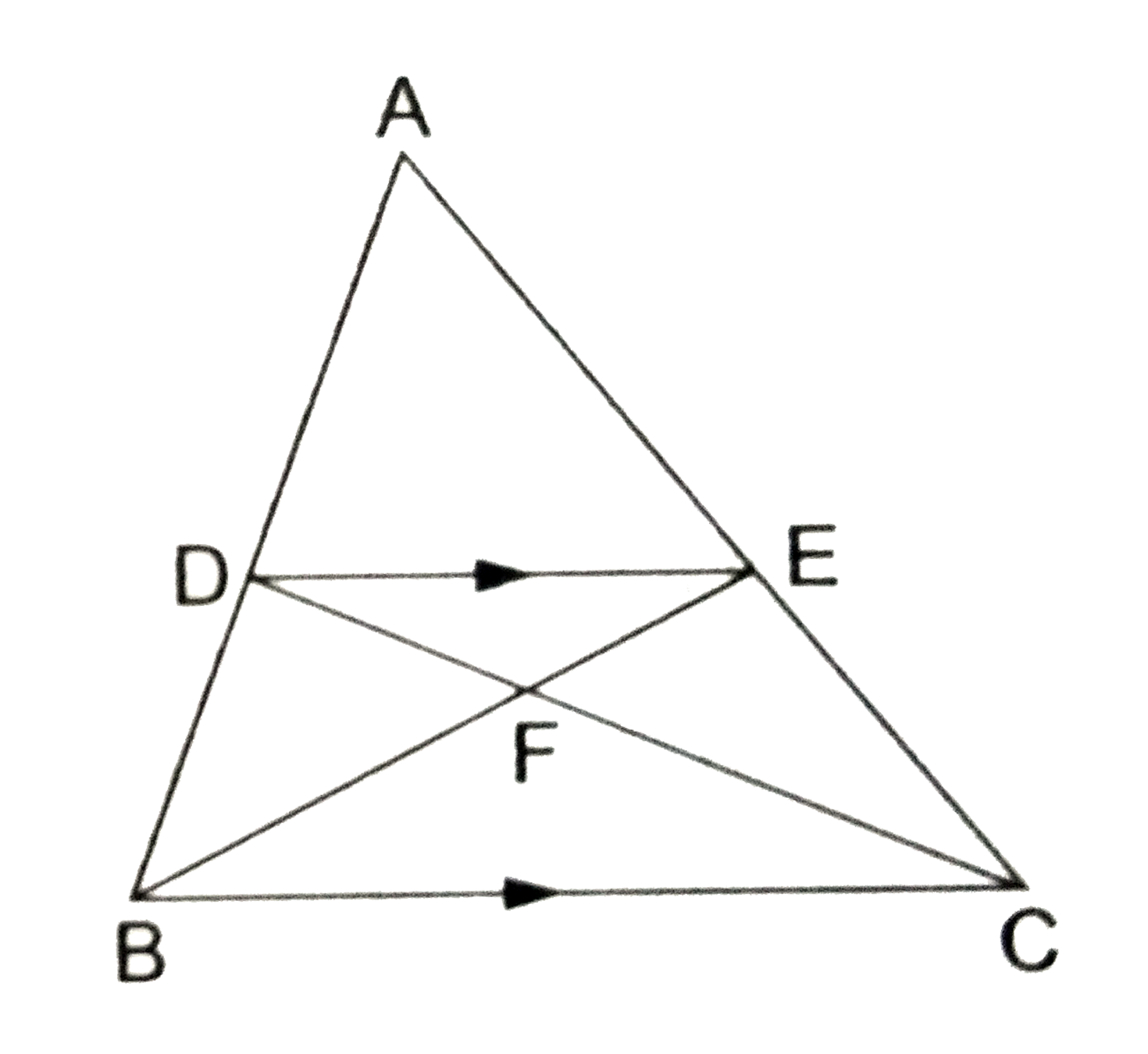
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
View SolutionIf ΔABC~ΔDEF and AB:PQ=5:7 then write the ratio of A(ΔABC):A(ΔPQR).
View Solution
