Consider a ΔPQR, in which PQ = 7 cm, QR= 25 cm, RP = 24 cm, then the triangle is right angled at
Q
R
P
can't say
To determine whether triangle PQR is right-angled and at which vertex, we can use the Pythagorean theorem. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
1. Identify the sides of the triangle:
- PQ = 7 cm
- QR = 25 cm (this is the longest side)
- RP = 24 cm
2. Assign the sides based on the Pythagorean theorem:
- In a right triangle, the longest side (hypotenuse) is opposite the right angle. Here, QR = 25 cm is the longest side.
3. Apply the Pythagorean theorem:
- According to the theorem:
QR2=PQ2+RP2
- Substitute the values:
252=72+242
4. Calculate the squares:
- Calculate QR2:
252=625
- Calculate PQ2:
72=49
- Calculate RP2:
242=576
5. Sum the squares of the other two sides:
- Now, add PQ2 and RP2:
49+576=625
6. Compare the results:
- We find that:
QR2=PQ2+RP2⇒625=625
- This confirms that the triangle is right-angled.
7. Determine the right angle's position:
- Since QR is the hypotenuse, the right angle must be at the vertex opposite the hypotenuse, which is point P.
Conclusion:
The triangle PQR is right-angled at point P.
- PQ = 7 cm
- QR = 25 cm (this is the longest side)
- RP = 24 cm
- In a right triangle, the longest side (hypotenuse) is opposite the right angle. Here, QR = 25 cm is the longest side.
- According to the theorem:
QR2=PQ2+RP2
- Substitute the values:
252=72+242
- Calculate QR2:
252=625
- Calculate PQ2:
72=49
- Calculate RP2:
242=576
- Now, add PQ2 and RP2:
49+576=625
- We find that:
QR2=PQ2+RP2⇒625=625
- This confirms that the triangle is right-angled.
- Since QR is the hypotenuse, the right angle must be at the vertex opposite the hypotenuse, which is point P.
The triangle PQR is right-angled at point P.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-B20videos
SAMPLE PAPER 10
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C10videos
SAMPLE PAPER 10
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -C10videos
SAMPLE PAPER 1
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)10videos
SAMPLE PAPER 10 (SELF-ASSESSMENT)
Similar Questions
Draw a ΔABC with AB = 4 cm, BC = 6 cm and CA = 3 cm. Draw another ΔPQR with PQ = 4 cm, QR = 6 cm and RP = 3 cm. State about the congruency of triangles.
 View Solution
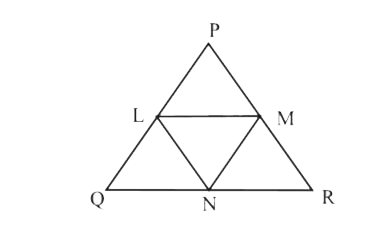
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In ΔPQR,PQ=6√3cm,PR=12cmandQR=6cm then ∠Q is
A45∘B60∘C90∘D120∘ - Question 2 - Select One
In ΔPQR,PQ=4 cm, PR = 6 cm and QR = 3 cm . Which of the following is correct ?
A∠R>∠QB∠Q>∠RC∠Q=∠RD∠R<∠P - Question 3 - Select One
In ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
A<Q=<RB<R<<PC<R><QD<Q><R
Consider the following statements :
Statement-I: Let PQR be a triangle in which PQ = 3 cm, QR = 4 cm and RP = 5 cm. If D is a point in the plane of the triangle PQR such that D is either outside it or inside it, then
DP+DQ+DR>6cm.
Statement-II : PQR is a right-angled triangle. Which one of the following is correct in respect of the above two statements ?View SolutionConstruct a triangle PQR in which QR = 6cm, ∠Q=60∘ and PR – PQ = 2cm.
View SolutionConstruct a triangle PQR such that PQ=6 cm, QR=7cm and PR=4.5cm.
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View SolutionLet △ABC~△RPQ and △ABC△RPQ=14, If PQ = 4 cmand PR = 7 cm, QR =6 cm, then AC is equal to:
मान लीजिये कि △ABC~△RPQ तथा △ABC△PQR=14 हैं | यदि PQ = 4 सेमी, BC = 4 सेमी और PR = 7 सेमी तथा QR - 6 सेमी है, तो AC का मान किसके बराबर है ?View Solution

