What will be the stress at −20∘C, if a steel rod with a cross-sectional area of 150 mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N. (Assume α=11.7×10−6/∘CandY=200×1011N/m2)
12.7×106N/m2
1.27×106N/m2
127×106N/m2
0.127×106N/m2
The correct Answer is:C
Let L= free length at 0∘C
L0 = final stretched length in each case. L1andL2 are free length at +20∘Cand−20∘C, respectively
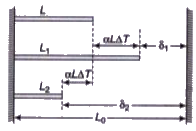
We know δ2=δ1+2αLΔT
Here, s1ands2 are load deformation
F2LAY=F1LAY+2αLΔT
σ=F2A=F1A+2αΔTY
=5000150×10−6+(2)(11.7×10−6)(20)(2×1011)
=127×106N/m2
Similar Questions
What will be the stress at −20∘C, if a steel rod with a cross-sectional area of 150 mm2 is stretched between two fixed points? The tensile load at 20∘C is 5000 N (Assume, α=11.7×10−6/∘C and Y = 200×1011N//m^(2))
View SolutionA steel rod with a cross-sectional area of 150mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N.
(a) What will be the stress at −20∘C ?
(b) At what temperature will the stress be zero ?
(Assume α=11.7μm/m∘C and Y=200GN/m2)
View Solution
Knowledge Check
A steel rod with a cross-sectional area of 150mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N.
(a) What will be the stress at −20∘C ?
(b) At what temperature will the stress be zero ?
(Assume α=11.7μm/m∘C and Y=200GN/m2)A12.7×106N/m2B1.27×106N/m2C127×106N/m2D0.127×106N/m2A wire of cross sectional area 3 mm2 is just stretched between two fixed points at a temperature of 20∘C . Then the tension in the wire when the temperature falls to 10∘C is,
(α=1.2×10−5/∘C,Y=2×1011N/m2)A80 NB60 NC72 ND50 NA wire of cross-sectional area 3mm2 is first stretched between two fixed points at a temperature of 20∘C. Determine the tension when the temperature falls to 10∘C Coefficient of linear expansion α=10−5.∘C−1andY=2×1011N/m2
A20 NB30 NC60 ND120 N
A steel rod with a cross-sectional area of 150mm2 is stretched between two fixed points. The tensile load at 20∘C is 5000N.
(a) What will be the stress at −20∘C ?
(b) At what temperature will the stress be zero ?
(Assume α=11.7μm/m∘C and Y=200GN/m2)
View SolutionA wire of cross sectional area 3mm2 is just stretched between two fixed points at a temperature of 20∘ . Determine the tension when the temperature falls to 20∘C . Coefficient of linear of expansion α=10−5/∘C and Y = 2×1011N/m2.
View SolutionA steel rod of length 50 cm has a cross–sectional area of 0.4cm2. What force would be required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C .
(α=10−5k−1 and Y=2×1011N/m2)
View SolutionA steel rod of length 25cm has a cross-sectional area of 0.8cm2 . The force required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C is (αsteel=10−5/∘C and Ysteel=2×1010N/m2)
View SolutionA steel rod of length 25cm has a cross-sectional area of 0.8cm2 . The force required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C is (αsteel=10−5/∘C and Ysteel=2×1010N/m2)
View Solution
