Question

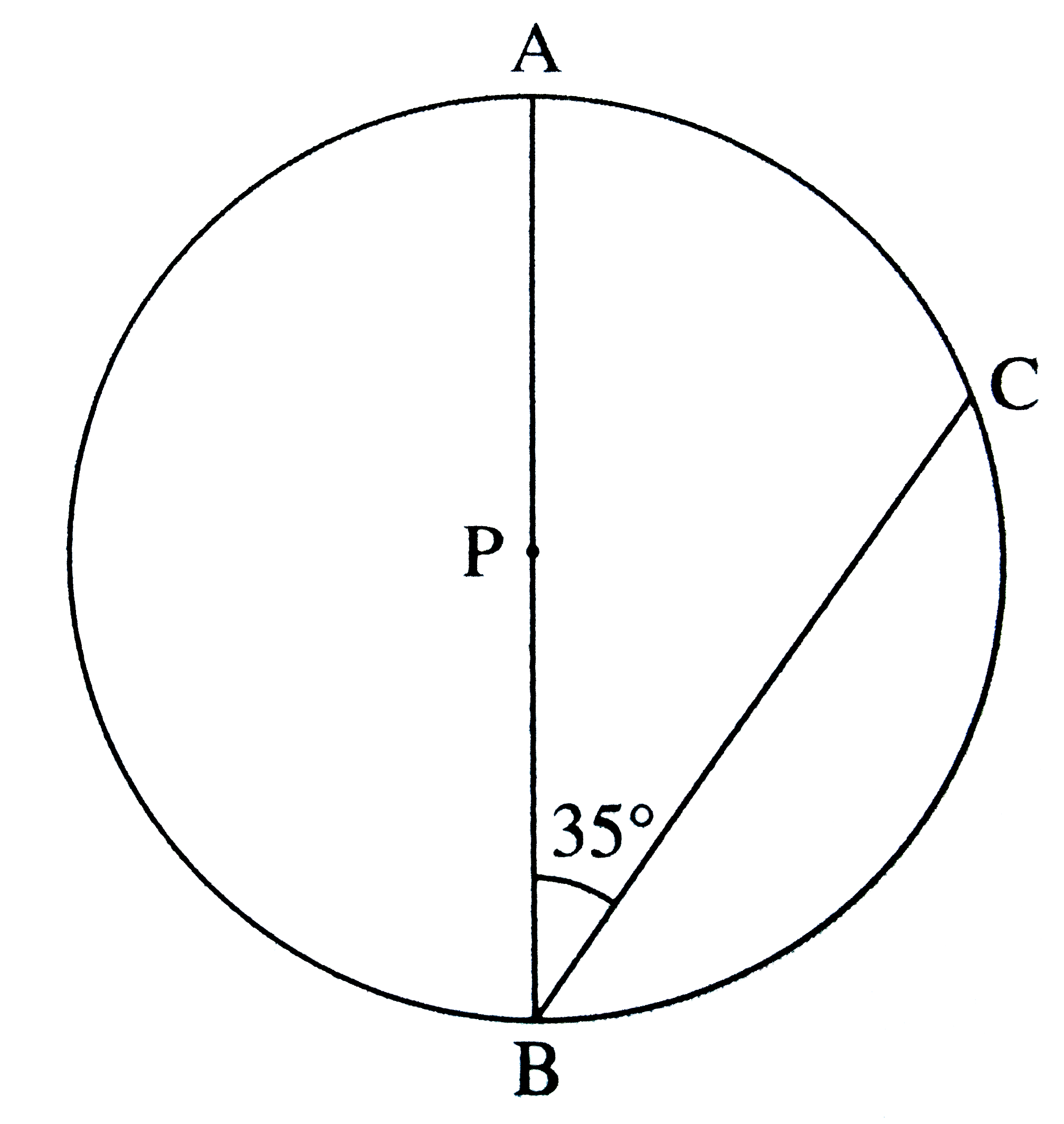
$△ABC$ is made on diameter in semicircle. Such that $\angle BAC={30}^{\circ }$, the value of $\angle BCA$ is

Options

A. `30`
B. `45^(@)`
C. `60^(@)`
D. `80^(@)`

Answer

C

Explanation

To solve the problem, we need to find the value of angle $$\angle BCA$$ in triangle $$△ABC$$ where $$△ABC$$ is inscribed in a semicircle with $$AB$$ as the diameter and $$\angle BAC={30}^{\circ }$$.

1. Understanding the Geometry:
- Since \( \triangle ABC \) is inscribed in a semicircle with \( AB \) as the diameter, we can use the property of angles in a semicircle. This property states that the angle opposite the diameter (in this case, \( \angle ACB \)) is a right angle (90 degrees).

Hint: Recall that any triangle inscribed in a semicircle has one angle equal to 90 degrees when the opposite vertex lies on the semicircle.

2. Identifying the Angles:
- We know \( \angle BAC = 30^\circ \) and \( \angle ACB = 90^\circ \).

Hint: Write down the known angles of the triangle to keep track of what you have.

3. Using the Triangle Angle Sum Property:
- The sum of the angles in any triangle is \( 180^\circ \). Therefore, we can write the equation:
\( \angle BAC + \angle ACB + \angle BCA = 180^\circ \)
Substituting the known values:
\( 30^\circ + 90^\circ + \angle BCA = 180^\circ \)

Hint: Remember the triangle angle sum property: \( \text{Sum of angles} = 180^\circ \).

4. Solving for \( \angle BCA \):
- Now we can simplify the equation:
\( 120^\circ + \angle BCA = 180^\circ \)
Subtract \( 120^\circ \) from both sides:
\( \angle BCA = 180^\circ - 120^\circ = 60^\circ \)

Hint: Isolate the variable to find the unknown angle.

5. Conclusion:
- Therefore, the value of \( \angle BCA \) is \( 60^\circ \).

Final Answer:
\( \angle BCA = 60^\circ \)