The volume of the solid generated by the revolution of the curve $y = \frac{a^{3}}{a^{2} + x^{2}}$ about x-axis is :

A

$\frac{1}{2} π^{3} a^{2}$

B

$π^{3} a^{2}$

C

$\frac{1}{2} π^{2} a^{3}$

D

$π^{2} a^{3}$

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Similar Questions

Given: the cycloid $x = a (t - sin t), y = a (1 - cos t), 0 \leq t \leq 2 π$
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]

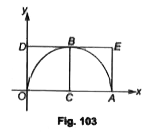
View Solution
Compute the volume of the solid generated by revolving about the x-axis the area bounded by the axes of coordinates and the parabola $x^{\frac{1}{2}} + y^{\frac{1}{2}} = a^{\frac{1}{2}}$ .
View Solution

Knowledge Check

The area bounded by the curve $a^{2} y = x^{2} (x + a)$ and the x-axis is
A $a^{2} / 3$ sq. units
B $a^{2} / 4$ sq. units
C $3 a^{2} / 4$ sq. units
D $a^{2} / 12$ sq. units

Recommended Questions

Home
Ask Doubt
Profile