Heat flows through two rods having same temperature difference at the ends. One rod is of length l1 and r1 and thermal conductivity K1 and the other rod of l2,r2 and K2 . The heat flow rate through the two rods will be equal, if
K1l2=K2l1
K1r21=K2r22
K1l2r1=K2l1r2
K1l2r21=K2l1r−22
The correct Answer is:D
Similar Questions
Two rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
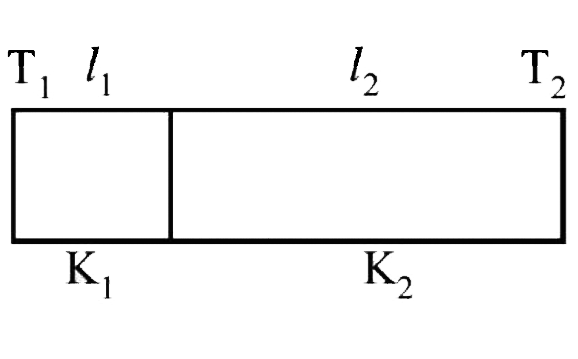
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View Solution
Knowledge Check
Two rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
AK1A2=K2A1BK1A1=K2A2CK1=K2DK1A1=K2A2One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
 AK1l1T1+K2l2T2K1l1+K2l2BK2l2T1+K1l1T2K1l1+K2l2CK2l1T1+K1l2T2K2l1+K1l2DK1l2T1+K2l1T2K1l2+K2l1
AK1l1T1+K2l2T2K1l1+K2l2BK2l2T1+K1l1T2K1l1+K2l2CK2l1T1+K1l2T2K2l1+K1l2DK1l2T1+K2l1T2K1l2+K2l1Two different metal rods of equal lengths and equal areas of cross-section have their ends kept at the same temperature θ1 and θ2. if K1 and K2 are their thermal conductivities, ρ1 and ρ2 their densities and S1 and S2 their specific heats, then the rate of flow of heat in the two rods will be the same if:
Ak1k2=ρ1s1ρ1s2Bk1k2=ρ1s2ρ2s1Ck1k2=θ1θ2Dk1=k2
Two metal rods 1 and 2 of the same length have same temperature difference between their ends. Their thermal conductivities are K1andK2 and cross-section areas A1andA2 respectively. What is the required condition for the same rate of heat conduction in them?
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionTwo adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
View SolutionTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
View Solution
