In ΔABC, the side AB is produced to E and side CA is produced to D. If ∠BAD=125∘and∠EBC=100∘, then which of the following is true ?
ΔABC is an isosceles triangle.
AB>BC
Difference between ∠ABCand∠ACB is 35∘
Difference between ∠BACand∠ACB is 20∘
To solve the problem, we will analyze the triangle ABC with the given angles and determine which of the provided statements is true.
1. Draw Triangle ABC:
- Start by sketching triangle ABC. Extend side AB to point E and side CA to point D.
2. Label the Angles:
- We know that angle BAD = 125° and angle EBC = 100°.
3. Find Angle ABC:
- Since angle EBC is on a straight line with angle ABC, we can use the property that angles on a straight line sum up to 180°.
- Therefore, angle ABC = 180° - angle EBC = 180° - 100° = 80°.
4. Find Angle ACB:
- Next, we can find angle ACB using the fact that angle BAD and angle ACB are supplementary (they form a linear pair).
- Thus, angle ACB = 180° - angle BAD = 180° - 125° = 55°.
5. Find Angle BAC:
- Now, we can find angle BAC using the triangle angle sum property, which states that the sum of the angles in a triangle is 180°.
- We already have angle ABC = 80° and angle ACB = 55°.
- Therefore, angle BAC = 180° - (angle ABC + angle ACB) = 180° - (80° + 55°) = 180° - 135° = 45°.
6. Check for Isosceles Triangle:
- An isosceles triangle has at least two equal angles. We have:
- Angle ABC = 80°
- Angle ACB = 55°
- Angle BAC = 45°
- Since none of the angles are equal, triangle ABC is not isosceles.
7. Evaluate the Options:
- Option 1: Triangle ABC is isosceles. (False)
- Option 2: AB is greater than BC. (Cannot be determined with the given angles)
- Option 3: The difference between angle ABC and angle ACB is 25°. (True, since 80° - 55° = 25°)
- Option 4: The difference between angle BAC and angle ACB is 0°. (False, since 45° - 55° = -10°)
Conclusion:
The true statement is that the difference between angle ABC and angle ACB is 25°.
- Start by sketching triangle ABC. Extend side AB to point E and side CA to point D.
- We know that angle BAD = 125° and angle EBC = 100°.
- Since angle EBC is on a straight line with angle ABC, we can use the property that angles on a straight line sum up to 180°.
- Therefore, angle ABC = 180° - angle EBC = 180° - 100° = 80°.
- Next, we can find angle ACB using the fact that angle BAD and angle ACB are supplementary (they form a linear pair).
- Thus, angle ACB = 180° - angle BAD = 180° - 125° = 55°.
- Now, we can find angle BAC using the triangle angle sum property, which states that the sum of the angles in a triangle is 180°.
- We already have angle ABC = 80° and angle ACB = 55°.
- Therefore, angle BAC = 180° - (angle ABC + angle ACB) = 180° - (80° + 55°) = 180° - 135° = 45°.
- An isosceles triangle has at least two equal angles. We have:
- Angle ABC = 80°
- Angle ACB = 55°
- Angle BAC = 45°
- Since none of the angles are equal, triangle ABC is not isosceles.
- Option 1: Triangle ABC is isosceles. (False)
- Option 2: AB is greater than BC. (Cannot be determined with the given angles)
- Option 3: The difference between angle ABC and angle ACB is 25°. (True, since 80° - 55° = 25°)
- Option 4: The difference between angle BAC and angle ACB is 0°. (False, since 45° - 55° = -10°)
The true statement is that the difference between angle ABC and angle ACB is 25°.
Similar Questions
The side BC of a triangle ABC is produced to D, bisector of the angle ABC and ACD meet at P. If ∠BPC=x∘ and ∠BAC=y∘, then which one of the following is correct ?
View SolutionThe sides AB and DC of a cyclic quadrilateral ABCD when produced meet at E and the sides DA and CB when produced meet at F. Given ∠BEC=38∘,∠BAD=102∘. Find the values of ∠AFB and ∠ADC.
View Solution
Knowledge Check
The sides AB and CD of a cyclic quadrilateral ABCD are produced to meet at P. The sides AD and BC are produced to meet at Q. If ∠ADC=85∘and∠BPC=40∘, then ∠BAD is equal to
 A45∘B30∘C95∘D55∘
A45∘B30∘C95∘D55∘I is the incentre of ΔABC,∠ABC=60∘ and ∠ACB=50∘. Then find ∠BIC.
A31B33C35D29ABCD is a cyclic quadrilateral in which sides AD and BC are produced to meet at P, and sides DC and AB meet at Q when produced. If ∠A=60∘ and ∠ABC=72∘ then ∠DPC−∠BQC=
ABCD एक चक्रीय चतुर्भुज है जिसमें भुजाओं AD तथा BC को बढ़ाया जाता है जो P पर मिलती हैं तथा भुजाओं DC और AB को बढ़ाया जाता है जो Q पर मिलती हैं | यदि ∠A=60∘ तथा ∠ABC=72∘ है, तो ∠DPC−∠BQC= ?A30∘B36∘C24∘D40∘
ΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
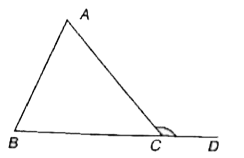
View SolutionIn the triangle ABC, side BC is produced to D. ∠ACD=100∘ if BC = AC. Then ∠ABC is :
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionThe side BC of ΔABC is produced to D. The bisectors of ∠ABCand∠ABD meet at E. If AB = AC and ∠BEC=24∘. then the measure of ∠ABC is :
View Solution