A steel rod of length 20326 is cut down from a rod of length 5615 what when is the remaining length of the rod?
363130
367130
3611130
361130
To find the remaining length of the steel rod after cutting down a portion from it, we will follow these steps:
1. Convert Mixed Numbers to Improper Fractions:
- The length of the steel rod is 20326.
- To convert this to an improper fraction:
20326=20×26+326=520+326=52326
- The length of the original rod is 5615.
- To convert this to an improper fraction:
5615=56×5+15=280+15=2815
2. Find a Common Denominator:
- The denominators are 26 and 5. The least common multiple (LCM) of 26 and 5 is 130.
- Convert both fractions to have a denominator of 130:
52326=523×526×5=2615130
2815=281×265×26=7296130
3. Subtract the Lengths:
- Now, subtract the length of the steel rod from the original rod:
Remaining Length=7296130−2615130=7296−2615130=4681130
4. Convert Back to Mixed Number:
- To convert 4681130 back to a mixed number:
- Divide 4681 by 130:
4681÷130=36(whole number part)
- Calculate the remainder:
4681−(36×130)=4681−4680=1
- Thus, the mixed number is:
361130
5. Final Answer:
- The remaining length of the rod is 361130.
- The length of the steel rod is 20326.
- To convert this to an improper fraction:
20326=20×26+326=520+326=52326
- To convert this to an improper fraction:
5615=56×5+15=280+15=2815
- The denominators are 26 and 5. The least common multiple (LCM) of 26 and 5 is 130.
- Convert both fractions to have a denominator of 130:
52326=523×526×5=2615130
2815=281×265×26=7296130
- Now, subtract the length of the steel rod from the original rod:
Remaining Length=7296130−2615130=7296−2615130=4681130
- To convert 4681130 back to a mixed number:
- Divide 4681 by 130:
4681÷130=36(whole number part)
- Calculate the remainder:
4681−(36×130)=4681−4680=1
- Thus, the mixed number is:
361130
- The remaining length of the rod is 361130.
Similar Questions
Knowledge Check
- Question 1 - Select One or More
A composite rod consists of a steel rod of length 25cm and area 2A and a copper rod of length 50cm and area A. The composite rod is subjected to an axial load F. If the Young's moduli of steel and copper are in the ratio 2:1 then
Athe extension produced in copper rod will be moreBthe extension in copper and steel parts will be in the ratio 1:2Cthe stress applied to copper rod will be moreDno extension will be produced in the steel rod - Question 2 - Select One
A brass rod of length 50cm and diameter 3.0cm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250∘C, if the original length are at 40.0∘C?
(Coefficient of linear expansion of brass =2.0×10−5/∘C,steel=1.2×10−5/∘CA0.27cmB0.34cmC0.21cmD0.18cm - Question 3 - Select One
The length of a rod is (11.05±0.05)cm. What is the length of two such rods?
A(22.1±0.05)cmB(22.10±0.05)cmC(22.1±0.10)cmD(22.10±0.10)cm
A brass rod length 50 cm and diamteer 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250∘C if the original length are at 40∘C ? Coefficient of linear expansion of brass and steel are 2.10×10−5.∘C−1 and 1.2×10−5^(∘)C−1 respectively.
View SolutionThe y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
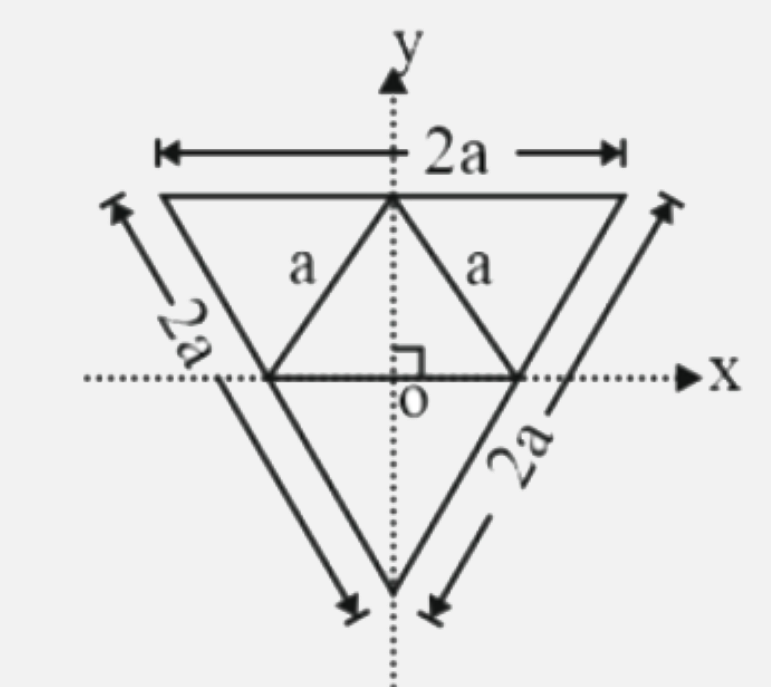 View Solution
View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.
 View Solution
View SolutionFind the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionRatio of energy density of two steel rods is 1:4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
View Solution

