15 small rods, each of length 2327 m are joined to make a big rod. What then is the length of the big rod?
34937m
34917m
34927m
34957m
To find the length of the big rod formed by joining 15 small rods, each of length 2327 meters, we can follow these steps:
Step 1: Convert the mixed number to an improper fraction
The length of each small rod is given as 2327. We can convert this mixed number into an improper fraction.
2327=(23×7)+27=161+27=1637
Step 2: Multiply the length of one rod by the number of rods
Now, we need to find the total length of the big rod by multiplying the length of one small rod by the number of rods (15).
Total Length=15×1637
Step 3: Perform the multiplication
We can multiply the fraction by the whole number:
Total Length=15×1637=24457
Step 4: Convert the improper fraction back to a mixed number
To convert 24457 back to a mixed number, we divide 2445 by 7.
2445÷7=349(with a remainder of 2)
This means:
24457=34927
Final Answer
Thus, the length of the big rod is 34927 meters.
---
The length of each small rod is given as 2327. We can convert this mixed number into an improper fraction.
Now, we need to find the total length of the big rod by multiplying the length of one small rod by the number of rods (15).
We can multiply the fraction by the whole number:
To convert 24457 back to a mixed number, we divide 2445 by 7.
Thus, the length of the big rod is 34927 meters.
Similar Questions
A steel rod of length 20326 is cut out from a rod of length 5615. What then is the remaining length of the rod?
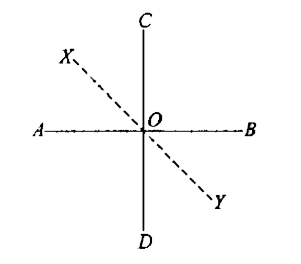
View SolutionAB and CD are two identical rods each of length l and mass m joined to form a cross. The moment of inertia of these two rods about a bisector (xy) of the angle between the rods is:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
AB and CD are two indential rods each of length L and mass M joined to from a cross. Find the M.L of the system about a bisector of the angel between the rods (XY):
 AML212BML26CML23D4ML23
AML212BML26CML23D4ML23 - Question 2 - Select One
Two rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
Aml2/12Bml2/6Cml2/3Dml2/2 - Question 3 - Select One
Two rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
Aml2/12Bml2/6Cml2/3Dml2/2
A steel rod of length 20326 is cut down from a rod of length 5615 what when is the remaining length of the rod?
View Solutionfour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionTwo rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20∘C, the length of the copper rod is 0.5 m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's modulus of steel. (The coefficient of linear expansion of copper, αc=1.6×10−5∘C and Young's modulus of copper is 1.3×1013N/m2).
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionThe length of a rod is 5×102 m , the order of magnitude of the length of the rod is
View Solution

