Prove that a diameter AB of a circle bisects all those chords which are parllel to the tangent at the point A.
Step by step video solution for Prove that a diameter AB of a circle bisects all those chords which are parllel to the tangent at the point A. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
A45∘B60∘C90∘D180∘
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
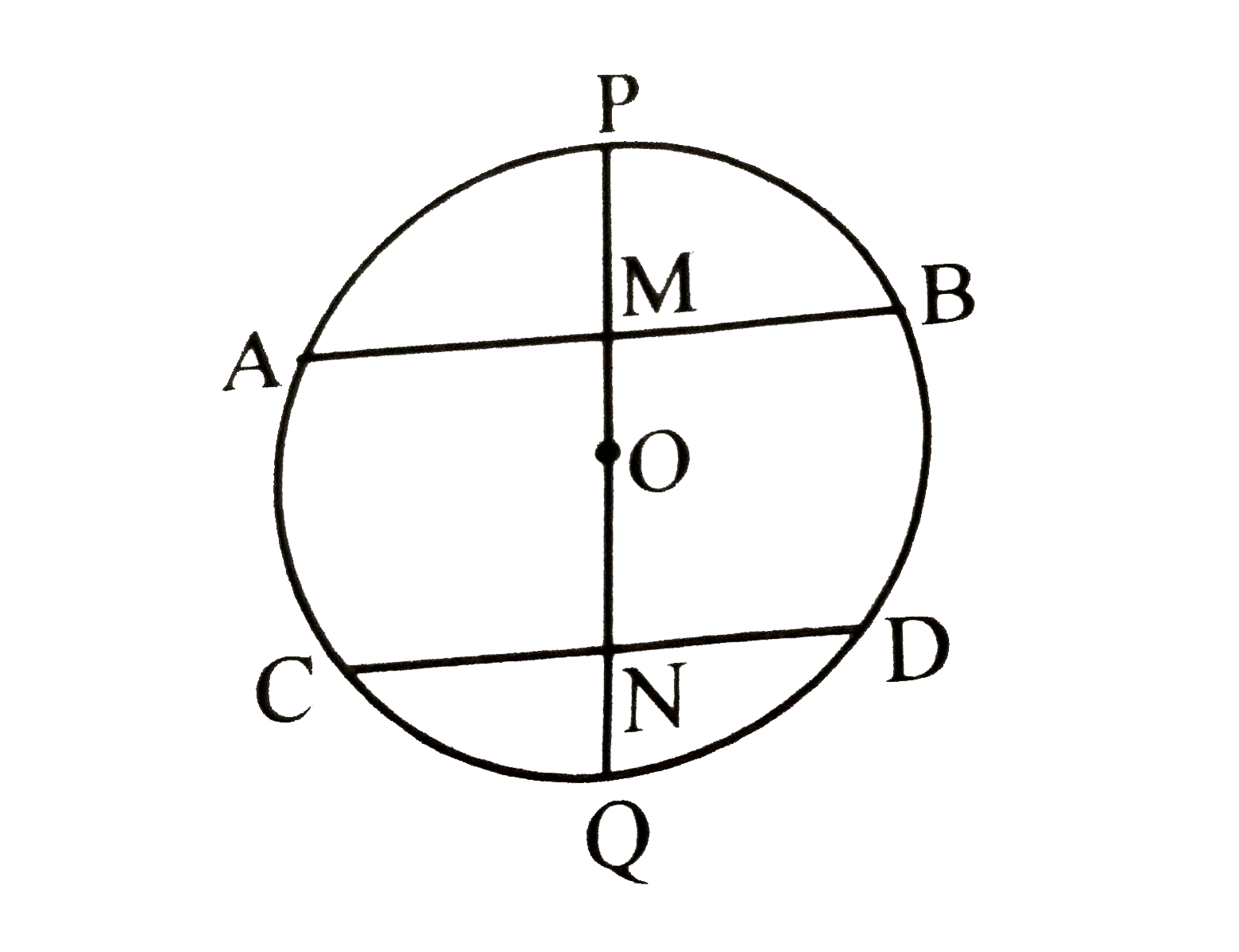
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD = AB. The tangent at B meets the line AC produced at E then AE is equal to
View SolutionIn the given figure, a diameter PQ of a circle bisects the chord RS at the point O. If PS is parallel to RQ, prove that RS is also a diameter of the circle.
View SolutionCircle described on the focal length as diameter touches the tangent at the vertex
View Solution
