Question

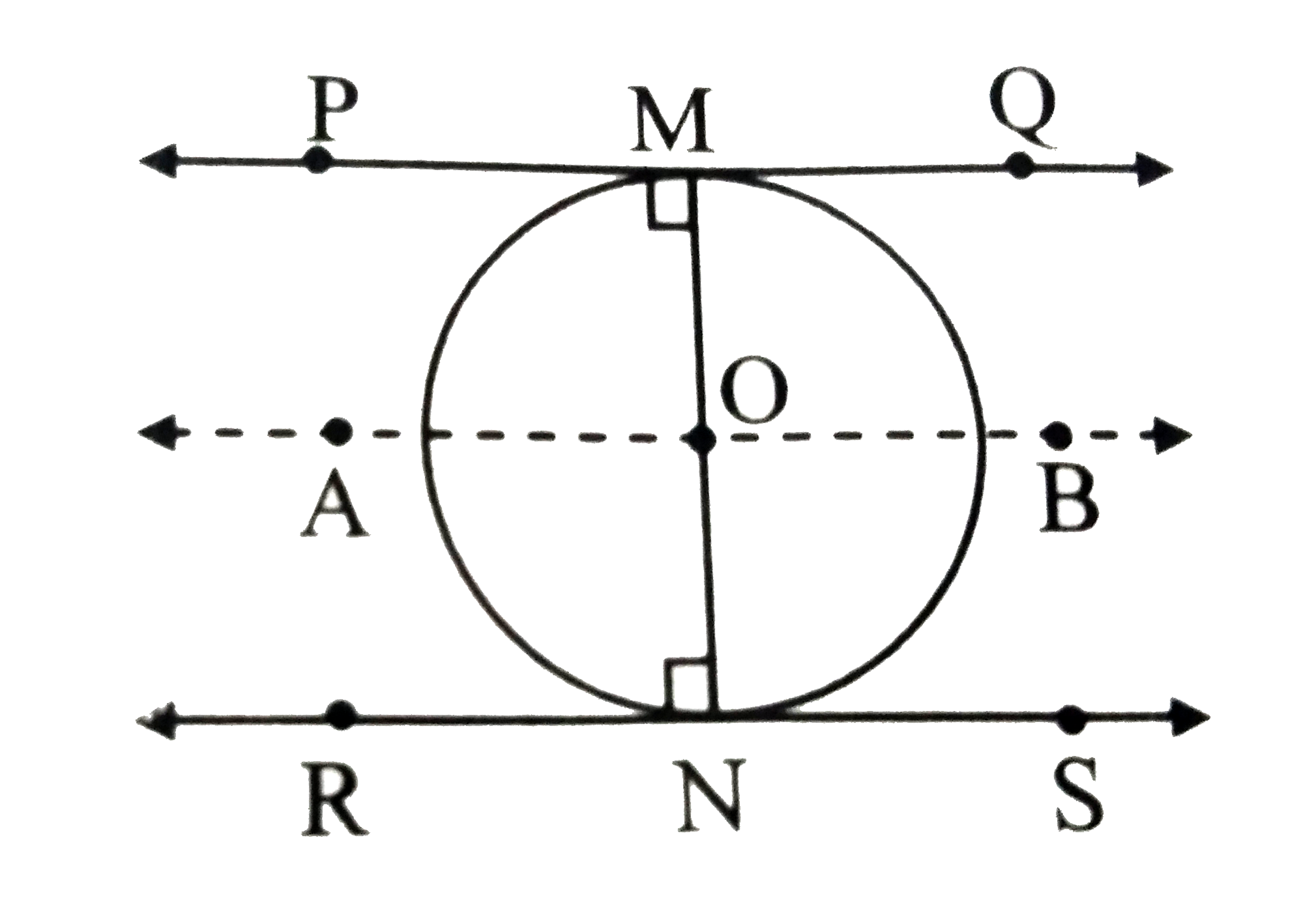
Find the distance between two parallel tangents of a circle whose radius is $3.5$ cm .

Options

A. 7 cm
B. `3.5 cm `
C. 10 cm
D. cannot be determined

Answer

A

Explanation

To find the distance between two parallel tangents of a circle whose radius is 3.5 cm, we can follow these steps:

1. Understand the relationship between radius and diameter:
The diameter (D) of a circle is twice the radius (R). The formula for diameter is:
\( D = 2R \)

2. Calculate the diameter:
Given that the radius (R) is 3.5 cm, we can substitute this value into the formula:
\( D = 2 \times 3.5 \text{ cm} = 7 \text{ cm} \)

3. Determine the distance between the parallel tangents:
The distance between two parallel tangents of a circle is equal to the diameter of the circle. Therefore, the distance between the two tangents is:
\( \text{Distance} = D = 7 \text{ cm} \)

Final Answer:
The distance between the two parallel tangents of the circle is 7 cm.

---