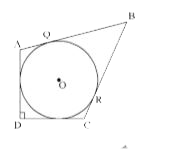
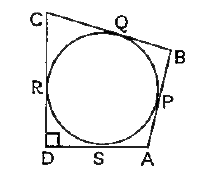
A circle is inscribed in the quadrilateral ABCD. Given BC= 38 cm . BQ= 27 cm , CD = 25 cm and ∠ADC=90∘ find the radius of the circle .
To find the radius of the circle inscribed in quadrilateral ABCD, we can follow these steps:
Step 1: Understand the problem
We have a quadrilateral ABCD with an inscribed circle. We know the lengths of some sides and segments:
- BC=38cm
- BQ=27cm
- CD=25cm
- ∠ADC=90∘
Step 2: Identify the segments
Since the circle is inscribed, the tangents drawn from an external point to the circle are equal. Thus, we have:
- BQ=BR=27cm (tangents from point B)
- Let CR=CS (tangents from point C)
Step 3: Calculate CR
Using the information that BC=BR+CR:
38=27+CR
Solving for CR:
CR=38−27=11cm
Step 4: Identify CS
Since CR=CS, we have:
CS=11cm
Step 5: Use the length of CD
We know that:
CD=DS+CS
Given CD=25cm and CS=11cm:
25=DS+11
Solving for DS:
DS=25−11=14cm
Step 6: Find the radius
Since OP=OS=DS (the radius of the circle), we have:
Radius=DS=14cm
Conclusion
The radius of the inscribed circle is 14cm.
---
We have a quadrilateral ABCD with an inscribed circle. We know the lengths of some sides and segments:
- BC=38cm
- BQ=27cm
- CD=25cm
- ∠ADC=90∘
Since the circle is inscribed, the tangents drawn from an external point to the circle are equal. Thus, we have:
- BQ=BR=27cm (tangents from point B)
- Let CR=CS (tangents from point C)
Using the information that BC=BR+CR:
38=27+CR
Solving for CR:
CR=38−27=11cm
Since CR=CS, we have:
CS=11cm
We know that:
CD=DS+CS
Given CD=25cm and CS=11cm:
25=DS+11
Solving for DS:
DS=25−11=14cm
Since OP=OS=DS (the radius of the circle), we have:
Radius=DS=14cm
The radius of the inscribed circle is 14cm.
Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Constructions) (VERY SHORT ANSWER TYPE QUESTIONS)
2 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Constructions) (Long Answer Type Questions)
16 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Circles) (Very short Answer type questions)
6 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Knowledge Check
In the adjacent figure, a circle is inscribed in the quadrilateral ABCD. If BC=38 cm, QB=27 cm, DC=25 cm and AD is perpendicular to DC then what is the radius of the circle ?
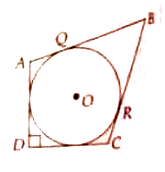 AA)11 cmBB)14 cmCC)15 cmDD)16 cm
AA)11 cmBB)14 cmCC)15 cmDD)16 cmA park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
A65.4cm2B69.4cm2C66.4cm2D68.4cm2The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
A720cm2B810cm2C1260cm2D2070cm2
In quadrilateral ABCD, angle D=90∘,BC=38cmanddc=25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27 cm. Find the radius of the circle.
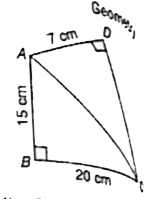
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
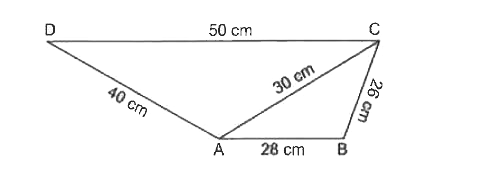
View SolutionIn the figure ∠ADC=90∘,BC=38cm,CD=28cmandBP=25cm
Find the radius of the circle.
View SolutionA circle is inscribed in a quadrilateral ABCD where ∠B=90∘If AD=24 cm AB=30 cm and DS= 8cm find the radius r of the incircle
View SolutionIn a quadrilateral ABCD , AB = 5 cm , BC = 37 cm , CD = 35 cm , BD = 12 cm , and AD = 13 cm . Find its area .
View Solution