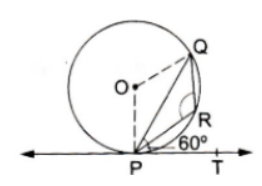
In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that $∠ Q P T = 60^{\circ} .$ Find $∠ P R Q .$

$105^{\circ}$

$115^{\circ}$

$120^{\circ}$

$130^{\circ}$

Video Solution

Answer

Step by step video & image solution for In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that angleQPT=60^(@).Find anglePRQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Circles Stage -2
1 Videos
NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Introduction to trigonometry Stage -1
2 Videos
NTSE 2019 -20BOOK - OSWAL PUBLICATIONCHAPTER - NTSE 2019 -20EXERCISE - Triangles Stage -2
1 Videos
NEW TYPOLOGIES INTRODUCED BY CBSE FOR BOARD 2021-22 EXAM BOOK - OSWAL PUBLICATIONCHAPTER - NEW TYPOLOGIES INTRODUCED BY CBSE FOR BOARD 2021-22 EXAM EXERCISE - UNIT-VII STATISTICS AND PROBABILITY (STATISTICS) (SELF ASSESSMENT)
2 Videos
OLYMPIAD 2019-20BOOK - OSWAL PUBLICATIONCHAPTER - OLYMPIAD 2019-20EXERCISE - 15. Probability
1 Videos

Knowledge Check

In the figure , PQ is a chord of a circle and PT is a tangent at P such that $∠ Q P T = 60^{\circ}, then ∠ P R Q$ =

A $100^{\circ}$
B $110^{\circ}$
C $120^{\circ}$
D $150^{\circ}$
In the adjoining figure , $O$ is the centre of the circle and $∠ O A B = 60^{\circ}$ . Find $∠ A P C$ .

A $= 60^{\circ}$
B $= 45^{\circ}$
C $= 30^{\circ}$
D $= 50^{\circ}$

In the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If $∠ Q P T = 60^{\circ}$ find $∠ P R Q$
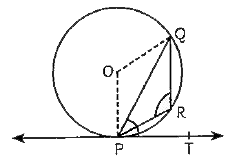
View Solution
In Figure PQ is a chord of a circle with centre O and PT is a tangent. If $Q P T = 60^{\circ}$ so, find PRQ.

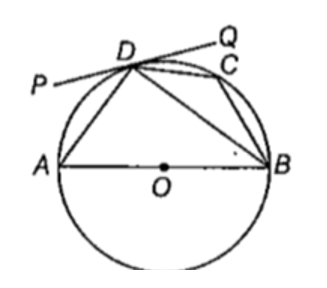
View Solution
In the adjoning figure O is the centre of the circle and AB is the diameter. Tangent PQ touches the circle at D. $∠ B D Q = 48^{\circ}$ . Find the ratio of angleDBA:angleDCB.
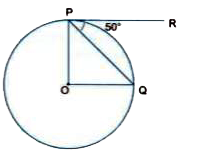
View Solution
In Fig , O is the centre of a circle , PQ is a chord and the tangent PR at P makes an angle of $50^{\circ}$ with PQ. Find $∠ P O Q$ .

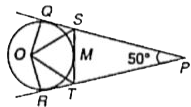
View Solution
In the adjoining figure 'O' is the centre of the circle and PQ, PR and ST are the three tangents. $∠ Q P R = 50^{\circ}$ , then the value of $∠ S O T$ is :

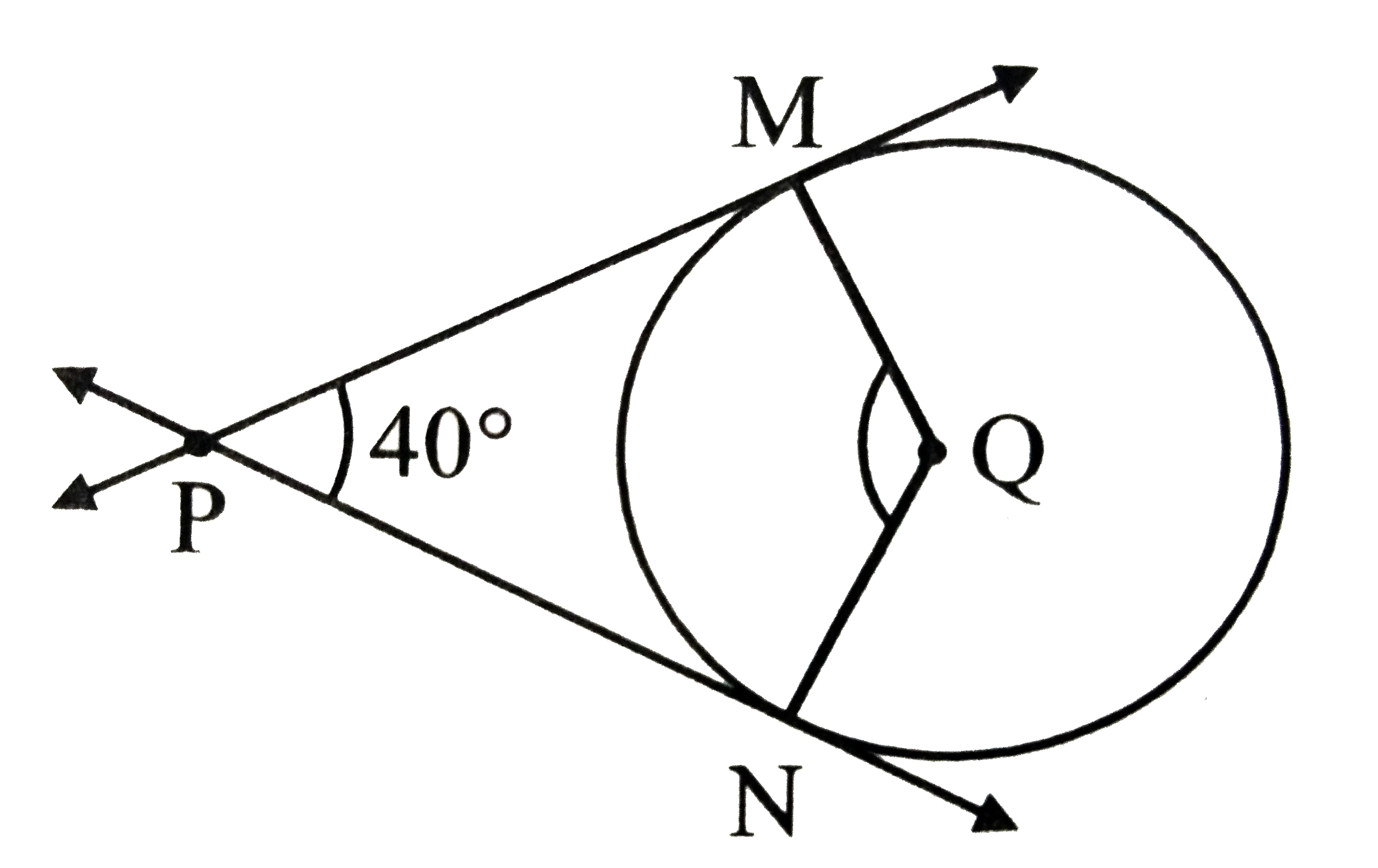
View Solution
In the adjoining figure , Q is the centre of the circle and PM,PN are tangent segments to the circle. IF $∠ M P N = 40^{\circ}$ , find $∠ M Q N$ .

View Solution

OSWAL PUBLICATION-NTSE 2019 -20-Circles Stage -1

In the figure what is mangleA =
01:45
In the adjoining figure, PQ is a chord of a circle and PT is the tange...
02:39

Home
Ask Doubt
Profile

In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =

In the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

OSWAL PUBLICATION-NTSE 2019 -20-Circles Stage -1

In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that $∠ Q P T = 60^{\circ} .$ Find $∠ P R Q .$

In the figure , PQ is a chord of a circle and PT is a tangent at P such that $∠ Q P T = 60^{\circ}, then ∠ P R Q$ =

In the adjoining figure , $O$ is the centre of the circle and $∠ O A B = 60^{\circ}$ . Find $∠ A P C$ .