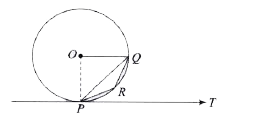
In the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘ find ∠PRQ
In the given figure,
∠QPT=60∘
∠QPO=∠OPT−∠QPT=90−60=30∘
As, OP=OQ,
∴∠OPQ=∠OQP=30∘
∴∠POQ=180−30−30=120∘
Now, ∠PRQ=12(360−∠POQ)=2402=120∘
Similar Questions
In the figure, ‘O’ is the centre of the circle and OM, ON are the perpendiculars from the centre to the chords PQ and RS. If OM = ON and PQ = 6cm. Find RS
View SolutionIn the figure 'O' is the centre of the circle ,PT is a tangent and if ∠PTO=30∘, find ∠POT

View SolutionIn the figure, PQ is a chord of a circle and PT is the tangent at P such that ⌊QPT=60∘. Find ⌊PRQ.

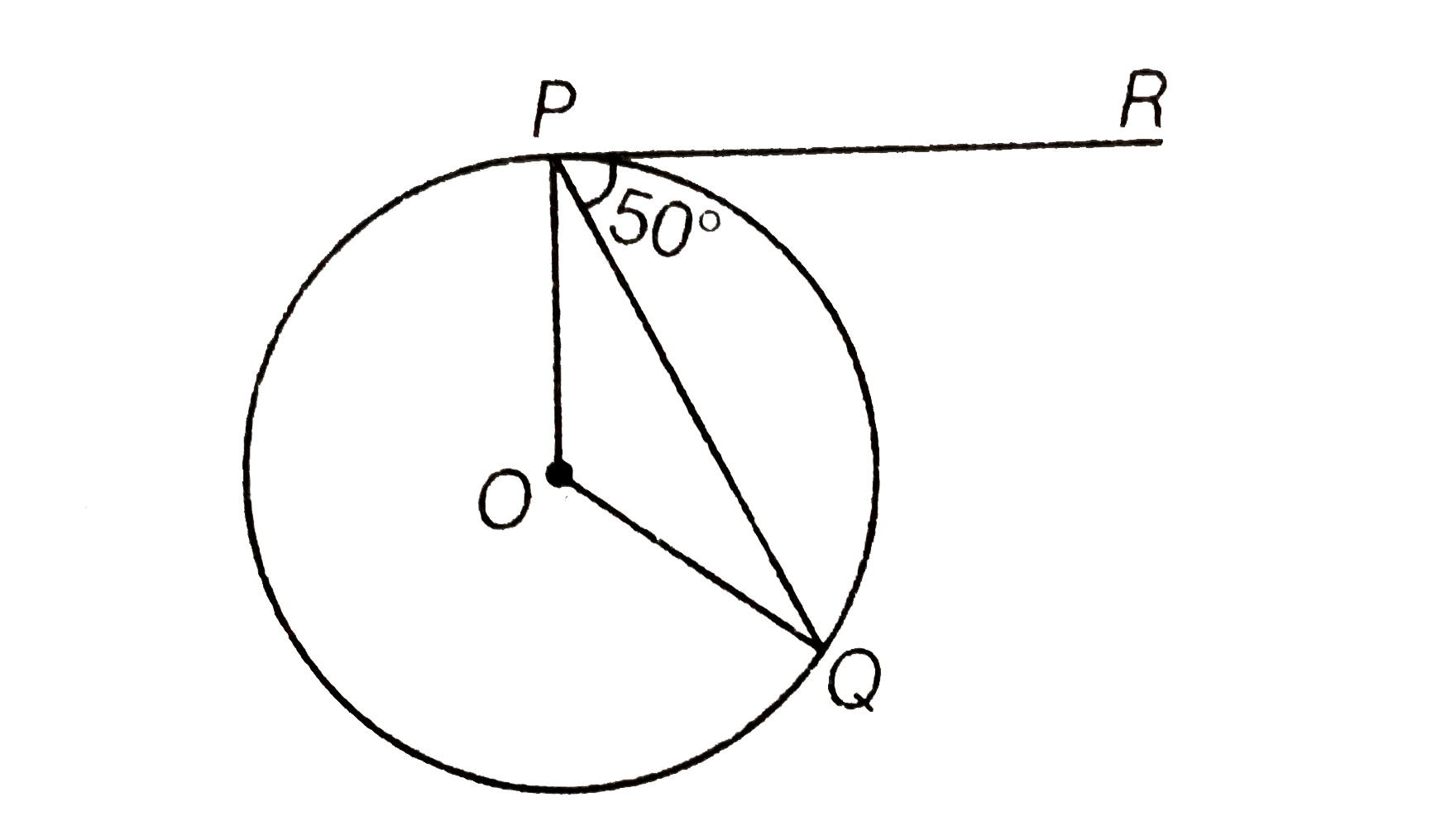
View SolutionIn figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
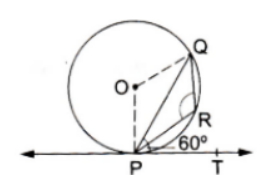
View SolutionIn the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
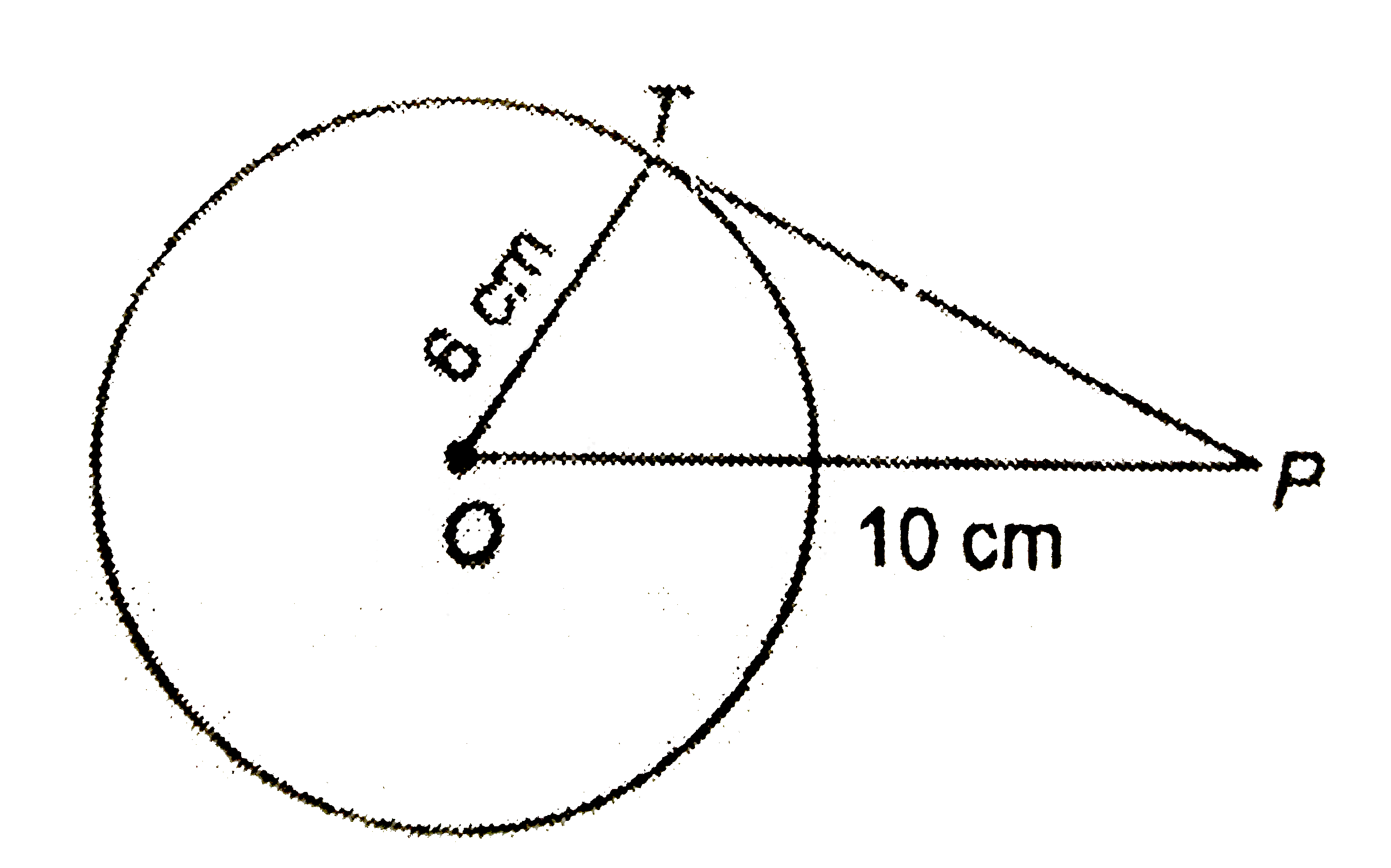
View SolutionIn the figure PT is a tangent to the circle with centre 'O' then x =
View SolutionIn the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
View Solution
