A glass slab made of a material of refractive index is kept in a medium of refractive index .
A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if
To solve the problem of drawing the path of a light ray emerging from a glass slab with a refractive index n1 in a medium of refractive index n2 (where n1>n2), we can follow these steps:
1. Identify the Setup:
- We have a glass slab with refractive index n1.
- The surrounding medium has a refractive index n2.
- Since n1>n2, the glass slab is denser than the surrounding medium.
2. Draw the Glass Slab:
- Draw a horizontal rectangle to represent the glass slab. Label the top part as the medium with refractive index n2 and the bottom part as the glass slab with refractive index n1.
3. Draw the Incident Ray:
- Draw a straight line approaching the glass slab at an angle. This line represents the incident ray. Label the point where it meets the glass slab as point A.
4. Draw the Normal Line:
- At point A, draw a vertical dashed line (normal line) perpendicular to the surface of the glass slab.
5. Label the Angles:
- Mark the angle of incidence i between the incident ray and the normal.
6. Apply Snell's Law at the First Interface:
- Since the light is moving from a rarer medium (air or medium with n2) to a denser medium (glass with n1), it will bend towards the normal. Use Snell's law:
n2sin(i)=n1sin(r)
where r is the angle of refraction inside the glass slab.
7. Draw the Refracted Ray Inside the Slab:
- From point A, draw a line inside the glass slab at angle r with respect to the normal. Label this line as the refracted ray.
8. Draw the Emergence Point:
- Mark the point where the refracted ray exits the glass slab. Label this point B.
9. Draw the Normal at the Emergence Point:
- At point B, draw another vertical dashed line (normal line) perpendicular to the surface of the glass slab.
10. Apply Snell's Law at the Second Interface:
- Now, the light ray is moving from the denser medium (glass with n1) to the rarer medium (medium with n2). According to Snell's law:
n1sin(r)=n2sin(e)
where e is the angle of emergence.
11. Draw the Emergent Ray:
- From point B, draw a line that makes an angle e with respect to the normal. This line represents the emergent ray.
12. Label the Angles:
- Note that the angle of incidence i at the first interface is equal to the angle of emergence e at the second interface.
Final Diagram:
- Your final diagram should show:
- The glass slab with the incident ray approaching it, bending towards the normal inside the slab, and then emerging and bending away from the normal as it exits into the rarer medium.
- We have a glass slab with refractive index n1.
- The surrounding medium has a refractive index n2.
- Since n1>n2, the glass slab is denser than the surrounding medium.
- Draw a horizontal rectangle to represent the glass slab. Label the top part as the medium with refractive index n2 and the bottom part as the glass slab with refractive index n1.
- Draw a straight line approaching the glass slab at an angle. This line represents the incident ray. Label the point where it meets the glass slab as point A.
- At point A, draw a vertical dashed line (normal line) perpendicular to the surface of the glass slab.
- Mark the angle of incidence i between the incident ray and the normal.
- Since the light is moving from a rarer medium (air or medium with n2) to a denser medium (glass with n1), it will bend towards the normal. Use Snell's law:
n2sin(i)=n1sin(r)
where r is the angle of refraction inside the glass slab.
- From point A, draw a line inside the glass slab at angle r with respect to the normal. Label this line as the refracted ray.
- Mark the point where the refracted ray exits the glass slab. Label this point B.
- At point B, draw another vertical dashed line (normal line) perpendicular to the surface of the glass slab.
- Now, the light ray is moving from the denser medium (glass with n1) to the rarer medium (medium with n2). According to Snell's law:
n1sin(r)=n2sin(e)
where e is the angle of emergence.
- From point B, draw a line that makes an angle e with respect to the normal. This line represents the emergent ray.
- Note that the angle of incidence i at the first interface is equal to the angle of emergence e at the second interface.
- Your final diagram should show:
- The glass slab with the incident ray approaching it, bending towards the normal inside the slab, and then emerging and bending away from the normal as it exits into the rarer medium.
Similar Questions
A glass slab made of a material of refractive index n1 is kept in a medium of refractive index n2.
A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n1=n2
View SolutionA glass slab made of a material of refractive index n1 is kept in a medium of refractive index n2. A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if (i) n1>n2 (ii) n1=n2 (iii) n1<n2.
View Solution
Knowledge Check
A rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
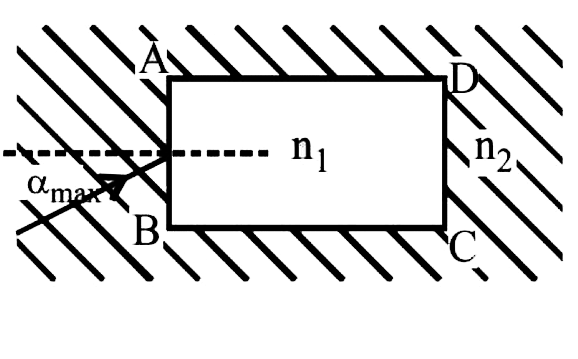 Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))A ray of light goes from a medium of refractive index n1 to a medium of refractive index n2. The angle of incidence is I and the angle of refraction is r. Then, sin i/sin r is equal to
An1Bn2C(n1)/(n2)D(n2)/(n1)A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
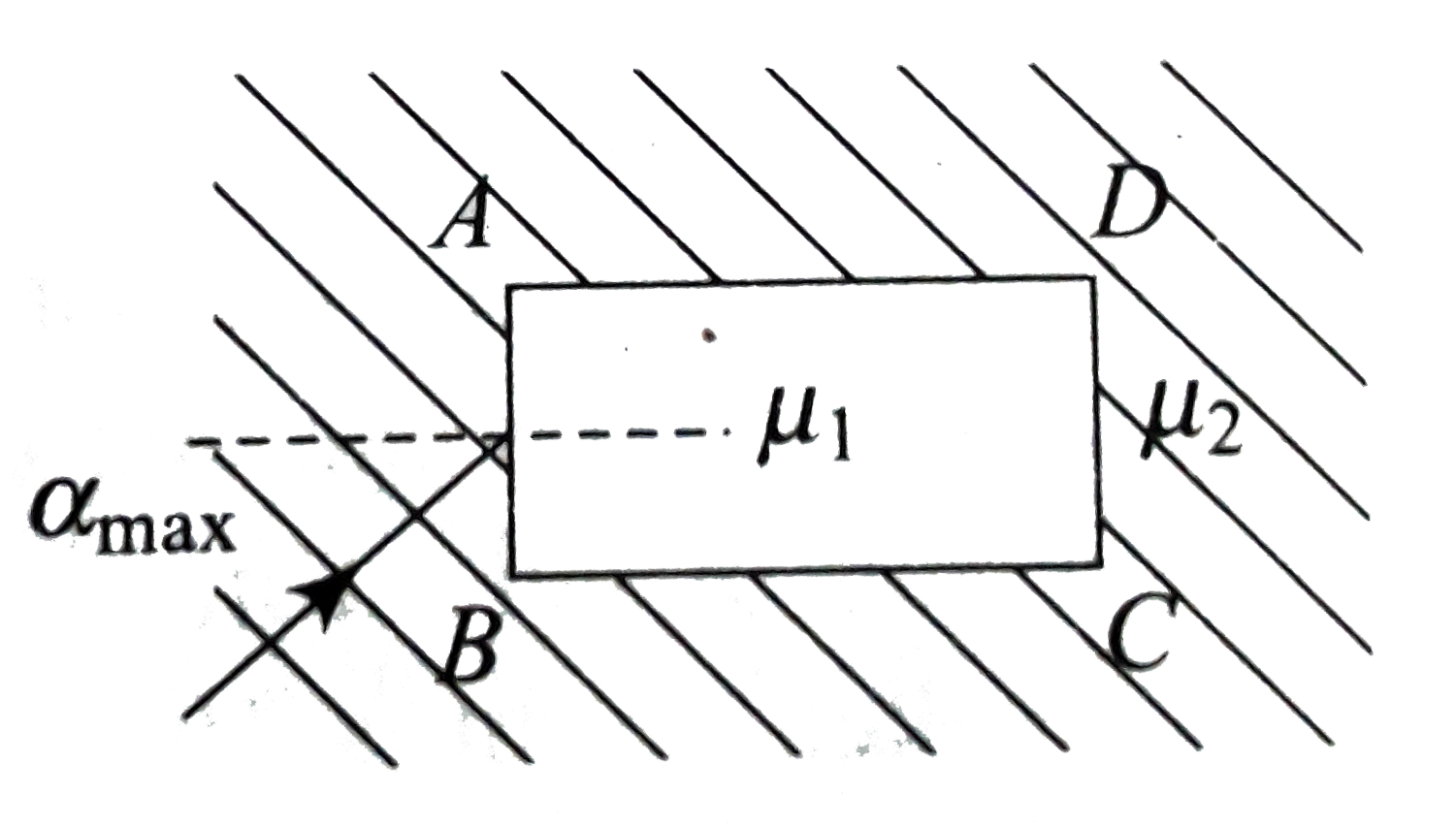 Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
A concave lens made of a material of refractive index n1 is kept in a medium of refractive index n2. A parallel beam of light is incident on the lens. Complete the path of rays of light emerging from the concave lens (i) n1>n2 (ii) n1=n2 (iii) n1<n2.
View SolutionA convex lens made of a material of refractive index n2 is kept in a medium of refractive index n1. A parallel beam of light is incident on the lens. Complete the path of rays of light emerging from the convex lens if
(i) n1<n2 (ii) n1=n2 (iii) n1>n2.
View SolutionThe refractive index of the material of a concave lens is nv It is immersed in a medium of refractive index n2. A parallel beam of light is incident on the lens. Trace the path of emergent rays
View SolutionThe refractive index of the material of a concave lens is n. It is immersed in a medium of refractive index n1. A paprallel beam of light is incident on the lens. Trace the path of emerged rays in each of the following cases :
(a) n1>n (b) n1<n ( c) n1=n.
View SolutionA rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
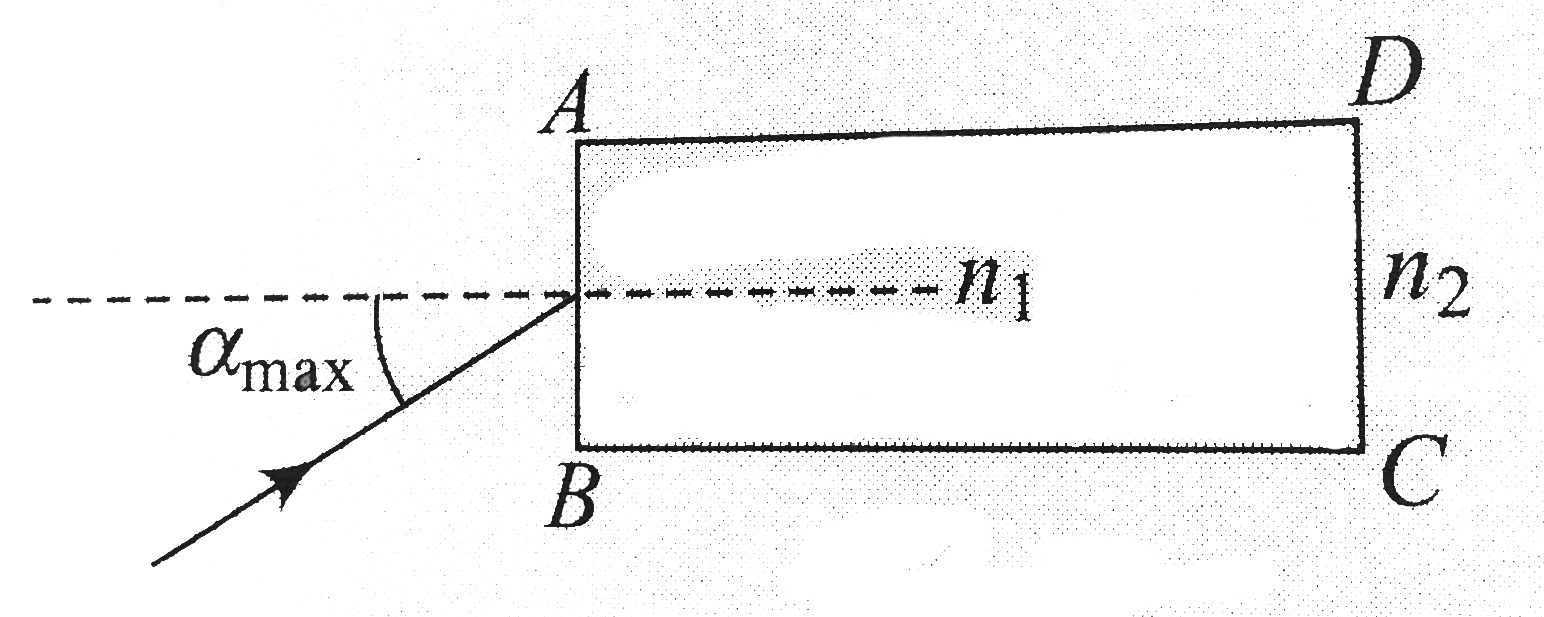
View Solution
