A glass slab made of a material of refractive index $n_{1}$ is kept in a medium of refractive index $n_{2}$ .
A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if $n_{1} = n_{2}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of a light ray passing through a glass slab when the refractive indices of the slab and the surrounding medium are equal, we can follow these steps:
1. Understand the Refractive Indices:
- We have a glass slab with a refractive index $n_{1}$ .
- The surrounding medium has a refractive index $n_{2}$ .
- Given that $n_{1} = n_{2}$ , both the glass slab and the medium are optically the same.
2. Draw the Glass Slab:
- Start by sketching a horizontal rectangle to represent the glass slab. Label the top of the slab as the air or surrounding medium and the bottom as the glass.
3. Incident Ray:
- Draw a straight line representing the incident ray approaching the glass slab at an angle. Label the angle of incidence as $i$ .
4. Refraction at the First Interface:
- Since $n_{1} = n_{2}$ , according to Snell's Law ( $n_{1} sin i = n_{2} sin r$ ), the angle of refraction $r$ will also equal $i$ . Thus, the ray will continue straight through the slab without bending.
5. Emergence from the Slab:
- As the ray reaches the second interface (the bottom of the slab), it will again follow Snell's Law. Since the refractive indices are equal, the ray will emerge at the same angle $i$ as it entered.
6. Final Path of the Ray:
- Draw the emergent ray continuing straight in the same direction as the incident ray. Label this angle as $e$ , which is equal to the angle of incidence $i$ .
Final Diagram:
- The diagram should show the incident ray entering the slab, the glass slab itself, and the emergent ray exiting the slab, all in a straight line.
Conclusion:
- The light ray passes through the glass slab without any deviation because the refractive indices of the two media are equal.

Updated on:8/8/2024

A rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index $n_{2} (n_{1} > n_{2})$ . A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence $α_{max}$ such that the ray comes out only from the other surface CD is given by
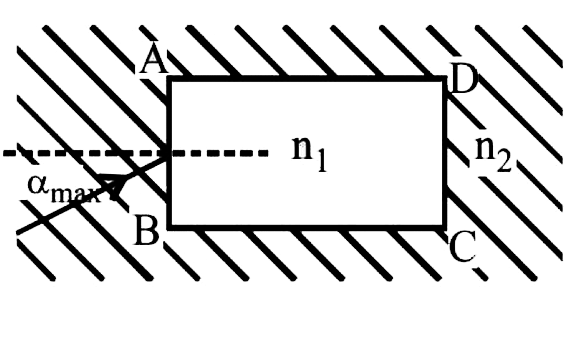A ${sin}^{- 1} [\frac{n_{1}}{n_{2}} cos ({sin}^{- 1} (\frac{n_{2}}{n_{2}}))]$
B ${sin}^{- 1} [n_{1} cos ({sin}^{- 1} (\frac{1}{n_{2}}))]$
C ${sin}^{- 1} (\frac{n_{1}}{n_{2}})$
Dsin^-1((n_2)/(n_2))
A ray of light goes from a medium of refractive index $n_{1}$ to a medium of refractive index $n_{2}$ . The angle of incidence is I and the angle of refraction is r. Then, sin i/sin r is equal to
A $n_{1}$
B $n_{2}$
C $(n_{1}) / (n_{2})$
D $(n_{2}) / (n_{1})$
A rectangular glass slab ABCD of refractive index $n_{1}$ is immersed in water of refractive index $n_{2} (n_{1} < n_{2})$ . A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence $α_{max}$ such that the ray comes out from the other surface CD is given by

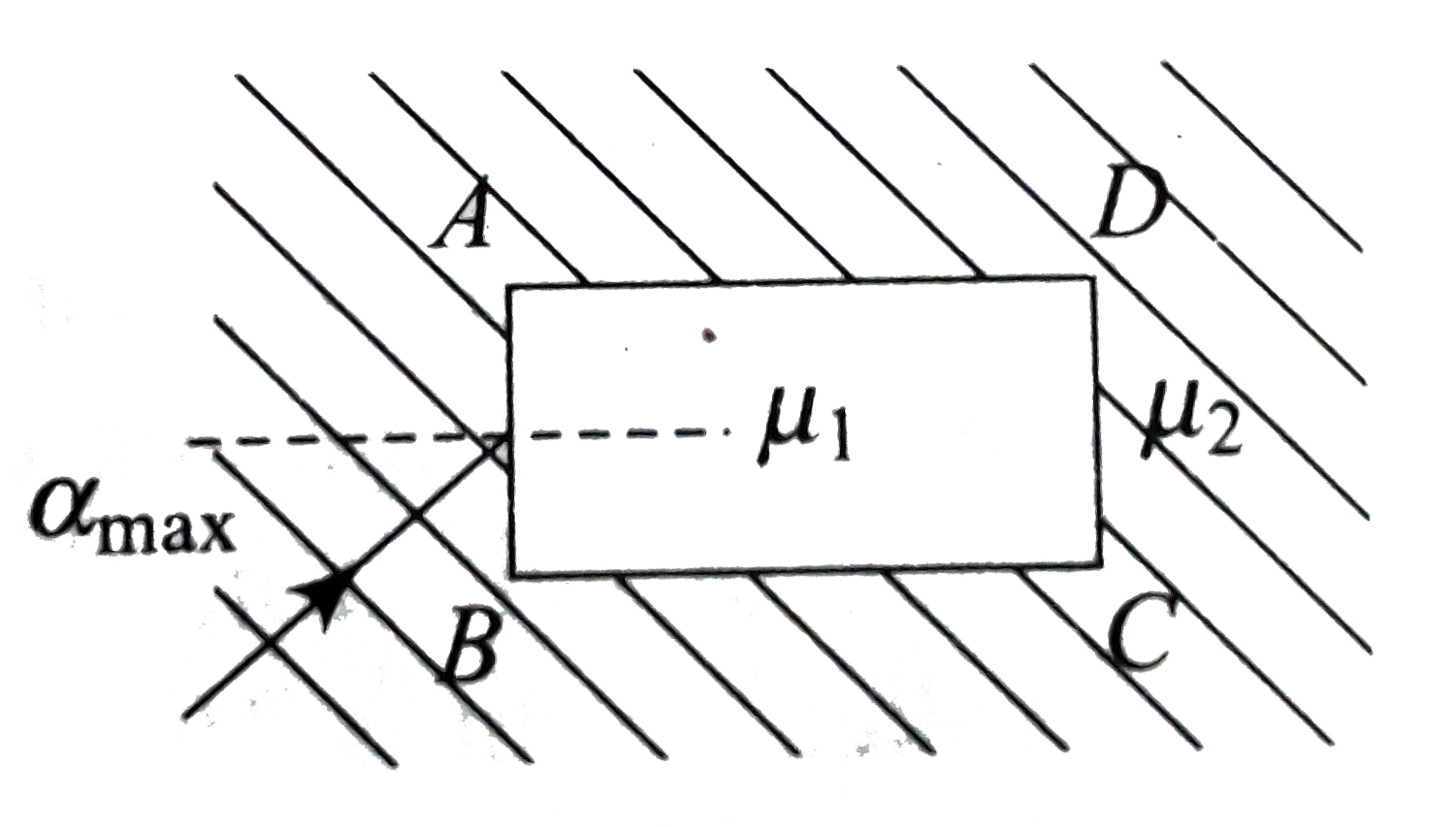A ${sin}^{- 1} [\frac{n_{1}}{n_{2}} cos ({sin}^{- 1} (\frac{n_{2}}{n_{1}}))]$
B ${sin}^{- 1} [n_{1} cos ({sin}^{- 1} (\frac{1}{n_{2}}))]$
C ${sin}^{- 1} (\frac{n_{1}}{n_{2}})$
D ${sin}^{- 1} (\frac{n_{2}}{n_{1}})$