In a rhombus ABCD, prove that AC2+BD2=4AB2
Step by step video & image solution for In a rhombus ABCD, prove that AC^(2) + BD^(2) = 4AB^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART A (SECTION-II)
8 Videos
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART B (SECTION-III)
8 Videos
- SAMPLE PAPER 11 (SELF - ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 11 (SELF - ASSESSMENT)EXERCISE - SECTION -C
10 Videos
- SAMPLE PAPER 2 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - D
9 Videos
Similar Questions
For a rhambus ABCD , prove that 4AB2=AC2+BD2
View SolutionIn a rhombus prove that sum of squares of sides is equal to sum of square of diagonals or, In a rhombus ABCD prove that
AB2+BC2+CD2+DA2=AC2+BD2
View SolutionIn rhombus ABCD, show that 4AB2=AC2+BD2
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
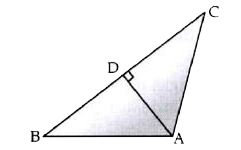
View SolutionABCD is a rhombus. Prove that AB2+BC2+CD2+DA2=AC2+BD2
View SolutionIn a quadrilateral ABCD prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2 where P and Q are middle points of diagonals AC and BD.
View SolutionIn a quadrilateral ABCD, prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2, where P and Q are middle points of diagonals AC and BD.
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View Solution
