For a rhambus ABCD , prove that 4AB2=AC2+BD2
To prove that for a rhombus ABCD, 4AB2=AC2+BD2, we can follow these steps:
Step 1: Understand the properties of a rhombus
A rhombus is a quadrilateral with all sides equal in length. The diagonals of a rhombus bisect each other at right angles.
Step 2: Label the rhombus and its diagonals
Let the diagonals AC and BD intersect at point O. Since the diagonals bisect each other, we have:
- AO=AC2
- BO=BD2
Step 3: Consider triangle AOB
In triangle AOB, we can apply the Pythagorean theorem because AO and BO are perpendicular to each other (as the diagonals bisect at right angles):
AB2=AO2+BO2
Step 4: Substitute the lengths of the segments
Substituting the expressions for AO and BO:
AB2=(AC2)2+(BD2)2
Step 5: Simplify the equation
Now, simplifying the right-hand side:
AB2=AC24+BD24
Step 6: Multiply through by 4
To eliminate the fractions, multiply the entire equation by 4:
4AB2=AC2+BD2
Conclusion
Thus, we have proved that:
4AB2=AC2+BD2
Hence proved.
---
A rhombus is a quadrilateral with all sides equal in length. The diagonals of a rhombus bisect each other at right angles.
Let the diagonals AC and BD intersect at point O. Since the diagonals bisect each other, we have:
- AO=AC2
- BO=BD2
In triangle AOB, we can apply the Pythagorean theorem because AO and BO are perpendicular to each other (as the diagonals bisect at right angles):
AB2=AO2+BO2
Substituting the expressions for AO and BO:
AB2=(AC2)2+(BD2)2
Now, simplifying the right-hand side:
AB2=AC24+BD24
To eliminate the fractions, multiply the entire equation by 4:
4AB2=AC2+BD2
Thus, we have proved that:
4AB2=AC2+BD2
Hence proved.
Topper's Solved these Questions
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - A (SECTION -II)
14 Videos
- SAMPLE PAPER 12 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 12 EXERCISE - PART - B (SECTION -III)
9 Videos
- SAMPLE PAPER - 6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 6 EXERCISE - PART - B (SECTION - IV)
13 Videos
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - V)
4 Videos
Similar Questions
In a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionIn rhombus ABCD, show that 4AB2=AC2+BD2
View SolutionIn a rhombus prove that sum of squares of sides is equal to sum of square of diagonals or, In a rhombus ABCD prove that
AB2+BC2+CD2+DA2=AC2+BD2
View SolutionIn a square ABCD, show that AC2=2AB2.
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2
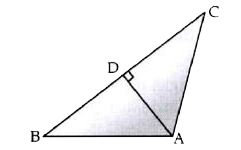
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionIn a quadrilateral ABCD, prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2, where P and Q are middle points of diagonals AC and BD.
View SolutionIn a ΔABC, ∠B is an acute-angle and AD⊥BC. Prove that:
AB2+CD2=AC2+BD2
View Solution
