From an external point Q, the length of the tangents to a circle is 5 cm and the distance of Q from the centre is 8 cm. The radius of the circle is:
39 cm
3 cm
√39 cm
7 cm
The correct Answer is:C
To find the radius of the circle from the given information, we can use the Pythagorean theorem. Here's a step-by-step solution:
Step 1: Understand the given information
We have:
- Length of the tangent from point Q to the circle (TQ) = 5 cm
- Distance from point Q to the center of the circle (OQ) = 8 cm
- We need to find the radius of the circle (OT).
Step 2: Set up the triangle
We can form a right triangle OQT, where:
- O is the center of the circle,
- T is the point of tangency,
- Q is the external point.
In this triangle:
- OQ is the hypotenuse,
- OT is one leg (the radius),
- TQ is the other leg (the length of the tangent).
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
OQ2=OT2+TQ2
Substituting the known values:
82=OT2+52
Step 4: Calculate the squares
Calculating the squares:
- OQ2=82=64
- TQ2=52=25
Step 5: Substitute and solve for OT
Now substituting the values back into the equation:
64=OT2+25
To find OT2, we rearrange the equation:
OT2=64−25
OT2=39
Step 6: Find the radius
Taking the square root of both sides to find OT (the radius):
OT=√39
Thus, the radius of the circle is √39 cm.
Final Answer
The radius of the circle is √39 cm.
---
We have:
- Length of the tangent from point Q to the circle (TQ) = 5 cm
- Distance from point Q to the center of the circle (OQ) = 8 cm
- We need to find the radius of the circle (OT).
We can form a right triangle OQT, where:
- O is the center of the circle,
- T is the point of tangency,
- Q is the external point.
- OQ is the hypotenuse,
- OT is one leg (the radius),
- TQ is the other leg (the length of the tangent).
According to the Pythagorean theorem:
OQ2=OT2+TQ2
82=OT2+52
Calculating the squares:
- OQ2=82=64
- TQ2=52=25
Now substituting the values back into the equation:
64=OT2+25
OT2=64−25
OT2=39
Taking the square root of both sides to find OT (the radius):
OT=√39
The radius of the circle is √39 cm.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Fill in the Blanks)9videos
CIRCLES
- BOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Write True or False)8videos
CIRCLES
- BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 2EXERCISE - Section -C7videos
CBSE TERM-1 SAMPLE PAPER 2
- BOOK - EDUCART PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - LONG ANSWER Type Questions6videos
CONSTRUCTIONS
Similar Questions
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
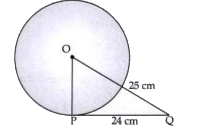 View Solution
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
View Solution
Knowledge Check
- Question 1 - Select One
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm, the radius of the circle is
A7 cmB12 cmC15 cmD24.5 cm - Question 2 - Select One
From an external point Q, the length of tangent to a circle is 12 cm and the distance of Q from the centre of circle is 13 cm. The radius of circle (in cm) is
A10B5C12D7 - Question 3 - Select One
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
A7 cmB12 cmC15 cmD24.5 cm
From a point Q, the length of the tangent to a circle is 40 cm and the distance of Q from the center is 41 cm. The radius of the circle is ______ cm
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cmView SolutionFrom a point Q, the length of the tangent to a circle is 12 cm and the distance of Q from the centre is 13 cm. The radius of the circle is 13 cm. The radius of the circle is :
View SolutionFrom a point A, the length of the tangent to ta circle is 24 cm . And the distance of a from the centre is 25 cm . The radius of the circle is
View Solution

