Question

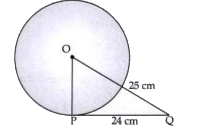
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.

Answer

Hence,radius of circle is 7 cm

Explanation

To find the radius of the circle given the length of the tangent and the distance from the point to the center, we can follow these steps:

1. Identify the Given Information:
- Length of the tangent (PQ) = 24 cm
- Distance from point Q to the center O (OQ) = 25 cm

2. Understand the Geometry:
- The tangent at point P is perpendicular to the radius OP at point P. Therefore, triangle OPQ is a right triangle with:
- OP as the radius (R)
- PQ as the length of the tangent
- OQ as the distance from the center to point Q

3. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem, in triangle OPQ:
\( OQ^2 = OP^2 + PQ^2 \)
- Substituting the known values:
\( 25^2 = R^2 + 24^2 \)

4. Calculate the Squares:
- Calculate \(25^2\) and \(24^2\):
\( 25^2 = 625 \)
\( 24^2 = 576 \)

5. Set Up the Equation:
- Substitute the squares into the equation:
\( 625 = R^2 + 576 \)

6. Isolate R²:
- Rearranging the equation to solve for \(R^2\):
\( R^2 = 625 - 576 \)
\( R^2 = 49 \)

7. Find the Radius R:
- Take the square root of both sides:
\( R = \sqrt{49} = 7 \text{ cm} \)

Final Answer:
The radius of the circle is 7 cm.